1) Calcule a área:
b) Da região .
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês?

Bora lá resolver mais uma questão!!
Nesse exercício, precisamos calcular a área formada por essa informação dada pelo enunciado. A área entre curvas é uma das principais utilizações das integrais, já que quando fazemos operações entre as curvas e integramos em um intervalo definido, encontramos a área formada entre elas.
Ou seja:
Essas funções que apareceram ( e ) serão as nossas curvas em questão. Já o intervalo são os pontos onde as curvas coincidem.
Legal, mas como fazemos isso? Como encontramos essa integral a ser calculada?
Apesar de parecer confusa, essa sentença toda nos fala o seguinte:
A região está em um plano que pertence ao , ou seja, em um plano dos números reais tanto para o eixo quanto para o eixo . Dentro desse plano, as funções que definem as nossas áreas são e .
Aqui temos as informações mais importantes até agora. Nossa área está definida nos valores de que são maiores ou iguais a na primeira função e nos valores de x que são menores ou iguais a na segunda função.
Ou seja, temos que calcular uma área entre 2 curvas! Legal, mas como fazemos isso?
A área entre curvas é uma das principais utilizações das integrais, já que quando fazemos operações entre as curvas e integramos em um intervalo definido, encontramos a área formada entre elas.
Ou seja:
Essas funções que apareceram ( e ) serão as nossas curvas em questão. Já o intervalo são os pontos onde as curvas coincidem.
Quando integramos uma função em , estamos calculando a área embaixo dessa curva no gráfico. Mas cuidado, que aqui a região ta sendo definida em , então o sinal que aparece antes da função na integral, vai ter a ver com o fato de a curva definir a região pela direita ou pela esquerda. Mas vamos ver isso com calma daqui a pouco!
Sabendo disso, só precisamos descobrir onde essas duas funções assumem valores iguais e, então, teremos qual o intervalo da nossa integração. E precisamos entender melhor essa região pra ver como fica o integrando.
Vamos calcular?
Passo 2
Como vimos no Passo 1, para encontrarmos o intervalo da nossa integração precisamos encontrar os pontos que as funções são iguais.
No nosso caso:
Como temos uma equação do segundo grau, precisamos encontrar as duas raízes. E elas serão:
Legal, definimos o intervalo de integração!
Passo 3
Antes de integrarmos, precisamos checar os gráficos das curvas para encontrarmos a melhor operação possível entre elas. Aqui definiremos se vamos somar ou subtrair as duas curvas na hora da integração.
Colocando as duas curvas em um gráfico vemos que:
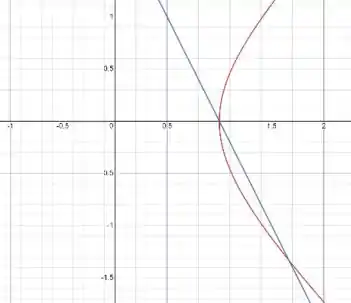
A linha vermelha define e a linha azul define . E queremos a área entre elas! Andando no eixo de para “encostamos” primeiro em , portanto essa função será .
A reta azul delimita a região de interesse pela direita. Considerando o sentido do eixo , calcular a integral dessa função, equivale a calcular a área a sua esquerda. Isso pode ser meio confuso, mas é tipo quando integramos uma função em e obtemos a área sob a curva. Mas aqui estamos integrando em , então vamos achar a área à esquerda da curva.
Já pra curva vermelha, a gente quer a área à direita. Então ela vai ser subtraída dentro da integral.
Vamos chamar então:
Colocando na fórmula que vimos no Passo 1, nossa integral fica assim:
Substituindo os valores:
Passo 4
Agora que encontramos a integral, só resta calcularmos! Como temos subtração entre os termos, podemos reescrever como:
Integrando:
Aplicando o intervalo:
Encontramos a área!
Ufaaa! Terminamos a questão!

Bora lá resolver mais uma então?