Calcule a área da região delimitada pelos gráficos das funções:
Passo 1
Não sei vocês mas essas funções malucas me deram calafrios! Mas relaxa que vamos tirar de letra. Um bom primeiro passo é o seguinte: toda vez que a gente quer uma área delimitada entre curvas, a gente vai precisar usar o ponto de interseção entre elas. Não acredita? Então olha só esse exemplo com funções mais amigáveis:
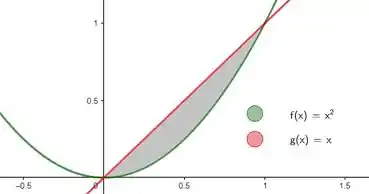
Show, então um bom primeiro passo será fazer:
O que resulta em:
O mesmo que:
Sabemos então o ponto em que as curvas se tocam, o que é importante porque na verdade esses serão os limites de integração!
Passo 2
Ok mas não acabamos ainda, temos que tomar muito cuidado com a posição relativa das funções. Afinal, no nosso exemplo amigável, estava por cima de o tempo todo, então a área seria algo do tipo:
Mas será que esse é o nosso caso? Bem, se estiver por cima, teremos que:
O que é essencialmente o que já fizemos, só que com um sinal de ao invés de . Ficamos então com:
Opa, isso é exatamente nosso intervalo de integração! Então ta confirmado que está por cima de no intervalo de integração inteiro! A área é modelada por:
Passo 3
Galera, agora é mão na massa, integrar, pegar o resultado, e partir pro abraço. Vamos ter como resultado:
Aplicando os limites de integração, temos
Feshow!