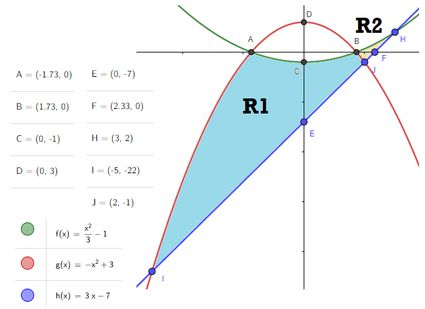
Q04) Seja a região compreendida entre os gráficos das funções , e . Faça o que se pede abaixo:
- Esboce a região , explicitando quais são os pontos de interseção entre as curvas.
- Escreva (mas não calcule!) integrais que representem a área de .
Passo 1
Essa questão parece complicada mas a gente consegue tirar de letra. Fica tranquilo porque se olharmos bem, e são só parábolas e é uma reta. Ou seja, são funções mais fáceis de esboçar, vamos só precisar prestar atenção nos pontos de interseção! Vamos ter pra :
Pra achar as coordenadas desses valores de podemos escolher tanto quanto . Acho que o é mais rápido então:
Marcamos então os pontos
Como é uma parábola com concavidade pra cima já que temos um número positivo multiplicando e uma parábola com concavidade pra baixo já que temos um número negativo multiplicando , podemos esboçar já elas duas. Mas antes, vamos ver as interseções com o eixo também:
Marcando os pontos encontrados e esboçando os gráficos temos:
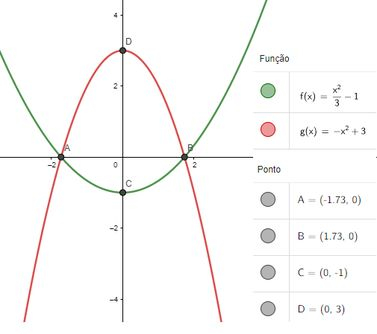
Passo 2
Ok, mas ta faltando algo né? A reta ! Vamos ver então quando ela toca nos eixos primeiro:
Agora, vamos ver quando ela toca com :
Olha lá, um polinômio de segundo grau! Usando então a fórmula de Bháskara pra achar as raízes desse polinômio, seja:
Onde:
Segundo a fórmula de Bháskara:
Vamos ter as seguintes raízes:
Logo:
Pra achar as coordenadas desses valores de podemos escolher tanto quanto . Acho que o é mais rápido então:
E agora pra fechar os pontos de interseção todos, vamos igualar a reta com . Sendo assim:
Eita, outro polinômio de segundo grau! Usando novamente a fórmula de Bháskara pra achar as raízes desse polinômio, onde:
Segundo a fórmula de Bháskara, teremos as seguintes raízes
Logo:
Pra achar as coordenadas desses valores de podemos escolher tanto quanto . Acho que o é mais rápido então:
Pronto, pegamos todos os pontos, agora bora marcar eles:
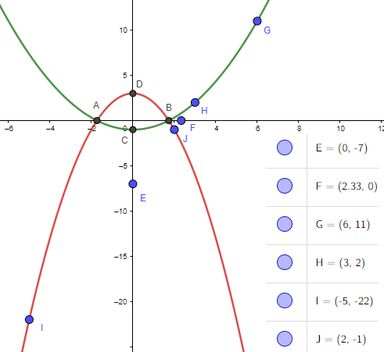
E traçando a reta:
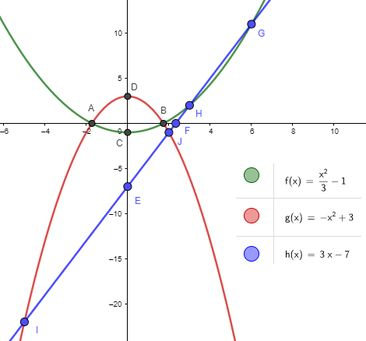
Passo 3
Agora que fechamos o esboço, vamos analisar direito os pontos todos pra ajudar a gente a entender as regiões:
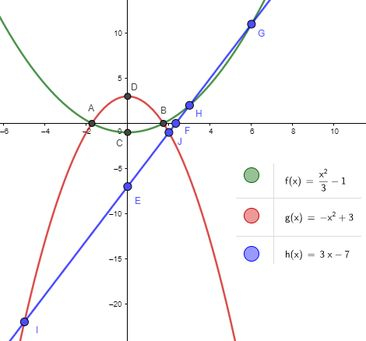
Pra começar, da pra ver que o G está lá em cima junto com H fecha uma região delimitada por e . Como não é isso que queremos, os dados desse ponto não vão ajudar a gente a entender a região, então vamos esquecer e dar um zoom na imagem nos outros pontos:
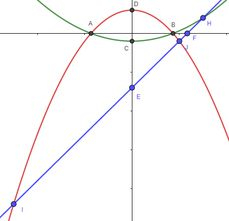
Essa questão na verdade tem dupla interpretação, pois você pode definir 2 regiões diferentes que são delimitadas pelas três funções ao mesmo tempo ou mesmo entender as duas regiões como uma só, da uma olhada:
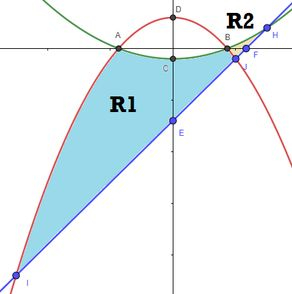
Então a letra já está respondida em! Vamos ter:
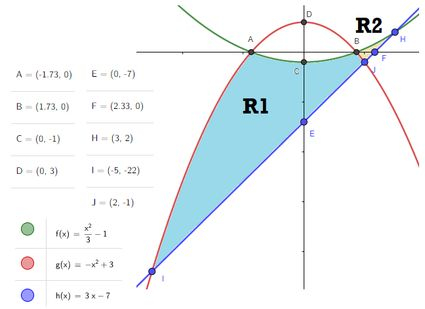
Passo 4
Agora o bicho pega. Vamos ter que pensar em fórmulas pra área de e . Vamos começar por . Pra fazer ela, vamos dividir em 2 pedaços, o pedaço R11 e R12:
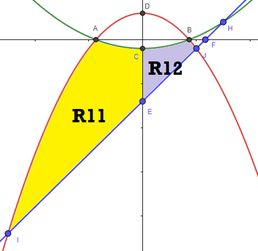
O pedaço R11 pode ser entendido como o pedaço subtraído dos pedaços e :
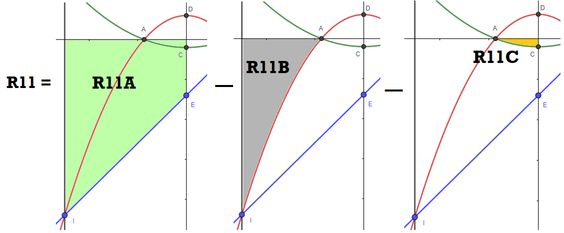
Só que são áreas diretas de calcular, só precisam de uma integral e em cada uma vai dentro uma das três funções diferentes ! Vamos ter:
Os sinais de negativo em cada pedaço estão aí pra compensar o resultado negativo do cálculo direto da integral. Os limites de integração vem das coordenadas dos pontos , e da origem. Vamos ter então:
O pedaço R12 pode ser entendido como o pedaço subtraído dos pedaços e :
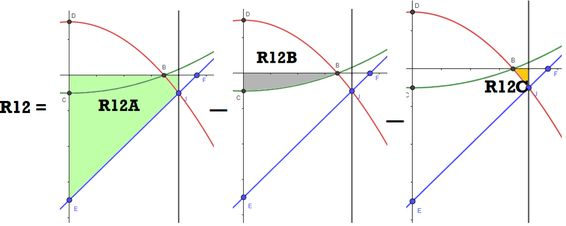
De novo, são áreas diretas de calcular que só precisam de uma integral e uma função dentro dela! Vamos ter:
Os sinais de negativo em cada pedaço estão aí pra compensar o resultado negativo do calculo direto da integral. Os limites de integração vem das coordenadas dos pontos , e da origem. Vamos ter então:
Juntando R11 e R12 pra dar a área de R1 temos:
Por fim
Passo 5
Falta agora a gente ver a área de R2. Brincando de LEGO de novo e juntando cada pedacinho da área, podemos entender R2 como:
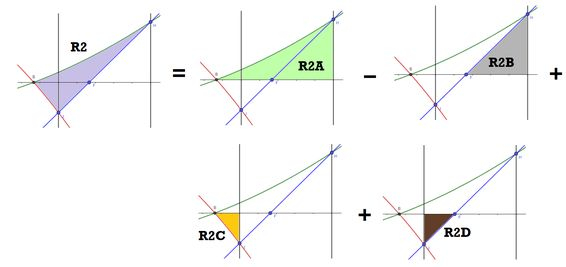
Sendo assim:
Onde cada pedaço são áreas diretas de calcular que só precisam de uma integral e uma função dentro dela! Vamos ter:
Os sinais de negativo em alguns pedaços novamente estão aí pra compensar o resultado negativo do calculo direto da integral. Os limites de integração vem das coordenadas dos pontos . Vamos ter então: