Considere a função dada por:
(a) Esboce o gráfico de
(b) Considere a região definida por:
Escreva a área de como uma soma de integrais na variável
Passo 1
(a) Esboçar o gráfico
Vamos lá, a questão pede pra gente esboçar o gráfico dessa função. Antes de mais nada, vamos lembrar da cara de uma função e :
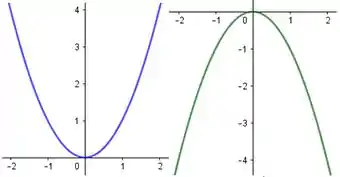
Parece um copo não é? A função do enunciado é também um copo porque assim como as funções acima, ela será tanto para quando para um polinômio de grau 2. Os outros termos só servem jogar o copo pra direita ou pra esquerda, pra cima ou pra baixo.
Então vamos lá, quando , vamos ter:
Como o está positivo, estamos falando de um copo como o azul: com a boca pra cima. Mas ele vai estar um pouco mais alto por causa do . Então vamos jogar o copo azul pra cima e ficamos com:
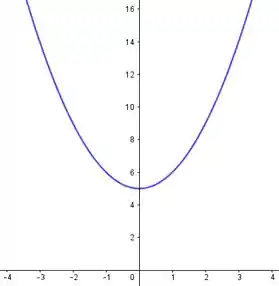
Mas como ele só é válido pra , então:
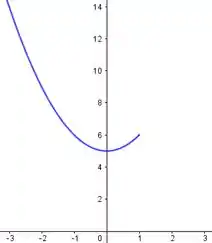
Agora, quando temos , nossa função vale:
Nesse caso, como o está negativo, estamos falando de um copo como o verde: com a boca pra baixo. Mas ele vai estar um pouco mais alto por causa do e um pouco mais pra direita por causa do . O copo verde então vai ficar:
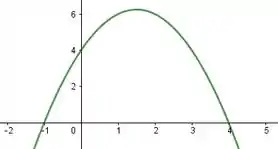
Mas como ele só é válido pra , então:
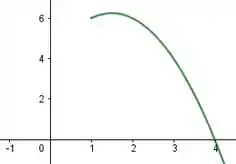
Juntando as duas curvas, temos:
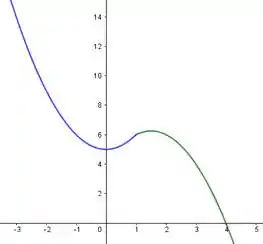
Passo 2
(b) Escrevendo a fórmula da área de
Como a região está entre a reta horizontal e a nossa função , graficamente, estamos falando da seguinte região:
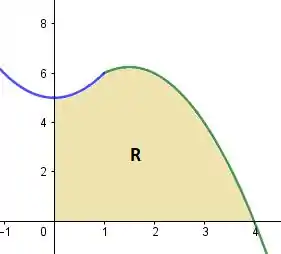
E o que é uma área se não a integral de uma função, dados os limites de integração, não é mesmo? Então:
Os limites de integração não temos ainda. Quer dizer, eles estão na figura mas finge que você não viu essa cola. Como acha-los?
O primeiro é fácil, porque o próprio enunciado deu. Se na região , então:
O segundo pelo esboço de gráfico a gente vê que deve ser a maior raiz de para . Então, vamos achar as raízes de . Simbora:
Pronto, achamos a maior raiz! Se a maior raiz é , então:
E nossa área fica:
Pra fechar, vamos lembrar que tem uma expressão diferente quando e quando . Deixamos clara essas expressões diferentes ao dividirmos a integral acima em duas. Então partiu!
Finito!
Resposta
(a)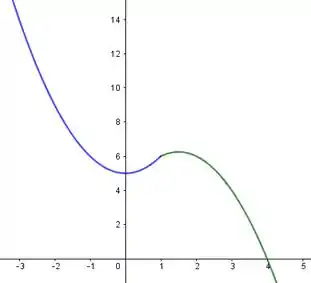
(b)