UFSC, Araranguá, Cálculo B, Listas de Cálculo B - Lista 102, Questão 14
Determine a área da região dentro do círculo e abaixo da reta .
Passo 1
Oiie, tudo bem?
Precisamos calcular a área da região entre as curvas polares
e
A região é tal que
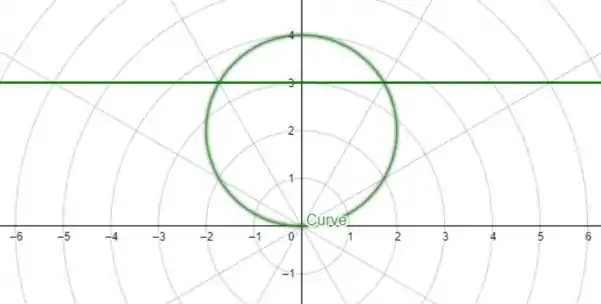
Ou seja, precisamos resolver uma integração da forma
em que é a função superior e é a função inferior! Vamos lá!
Passo 2
Os nosso limite de integração são obtidos para os valores em que as curvas se interceptam, ou seja, quando
como temos que
temos que o vínculo é tal que
ou, simplesmente
ou seja, temos que o nosso ângulo vai de até , e a integral se torna
Vamos resolver essas integrais! Saca só!
Passo 3
A primeira integral é bastante direta pois temos que a primitiva pode ser identificada lembrando que a derivada da cotangente é o negativo da cossecante ao quadrado, portanto
usando que , portanto, temos que
Agora, para a segunda integral, vamos precisar de algumas relações trigonométricas! Vamos lá!
Passo 4
Temos que resolver
usando que
podemos escrever que
Usando os resultados conhecidos
ou simplesmente
e, para a outra integral
que se resume à
De forma que a integral desejada é
Vamos juntar todos os resultados agora e obter a nossa área!
Passo 5
Coletando os resultados dos passos anteriores, temos que
portanto, temos que a área é igual à
A questão foi isso! te vejo na próxima! Tchau Tchau!