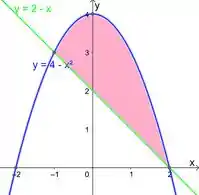
Esboce a região do plano delimitada pelos gráficos e e calcule sua área.
Passo 1
Cara, para esboçar essa região, a gente precisa esboçar as curvas e no mesmo plano, e identificar a região que está entre elas, beleza? E como a gente faz isso?
Nossas funções são:
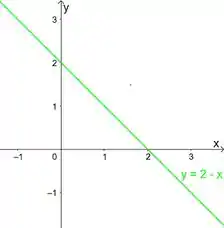
Essa primeira é uma reta. Para colocar ela no gráfico a gente só precisa de pontos. Se a gente fizer , achamos ; e se fizermos , achamos . Aí vemos que a reta passa pelos pontos:
Colocando no gráfico, fica assim:
E é uma parábola virada para baixo. Uma forma de localizá-la é achando achar pontos que pertencem a ela: os pontos onde ela corta os eixos coordenados.
- para , : ponto
- e para achar as raízes dessa parábola, fazemos
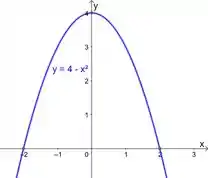
Então temos os pontos . Fazendo uma parábola virada para baixo que passa por esses pontos, a gente tem:
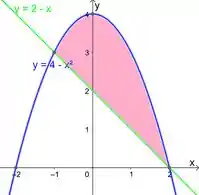
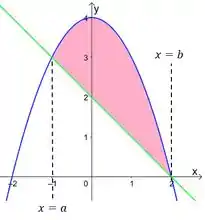
Colocando essas duas coisas no mesmo plano, e marcando a região entre elas, achamos essa região aqui:
Passo 2
E para achar a área entre curvas que são funções de , a gente precisa montar a fórmulinha:
A representa a função que limita a nossa região por cima, e a função que limita a nossa região por baixo.
Olhando ali no nosso desenho, vemos que quem limita nossa região por cima é a e quem limita nossa região por baixo é a função .
Aí a gente tem que para o nosso caso:
E nosso integrando fica:
Passo 3
E na fórmula, é o intervalo em que nossa região está. A gente vê que ela está entre os dois valores de das interseções entre essas duas curvas. Vamos achar esses caras!
A gente tem
Igualando essas duas expressões para :
Daí a gente tira que:
E aí a nossa integral para calcular a área fica:
Passo 4
Agora é calcular essa belezura.
Uma propriedade diz que podemos fazer a integral de cada uma das funções e depois fazer a subtração e a soma entre elas:
Usando a regrinha de integrar polinômios:
Resposta