Sejam tais que então:
- Teremos sempre que
- Teremos sempre que
- Podemos ter
- Teremos sempre que
- Podemos ter
Passo 1
Show, bora começar. Antes de mais nada, uma forma legal da gente resolver essa questão é pensar nos casos possíveis em que uma função sobre a outra pode tender à . Da propriedade dos limites, temos que:
Beleza, se usarmos essa propriedade, podemos ver alguns casos interessantes que dão na mesma. Saca só:
Exemplo:
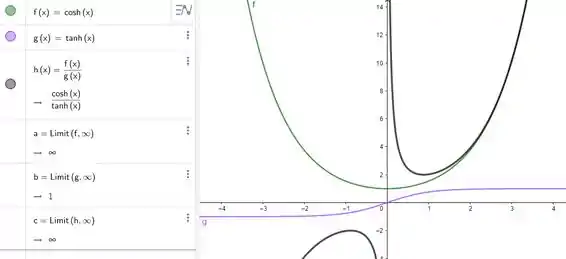
Exemplo:
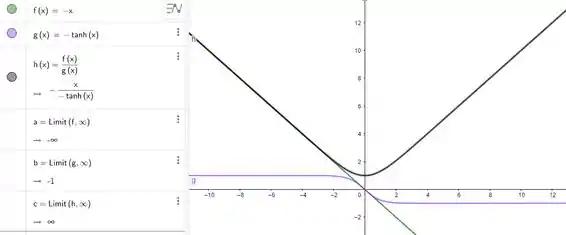
Exemplo:
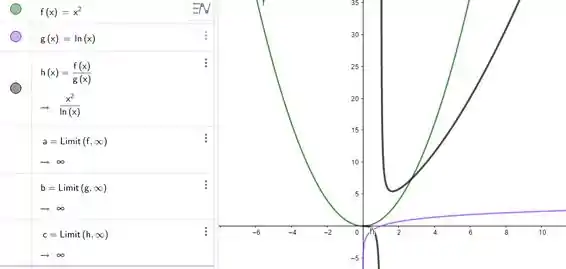
Exemplo:
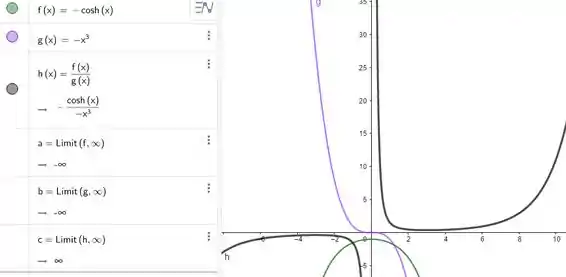
Exemplo:
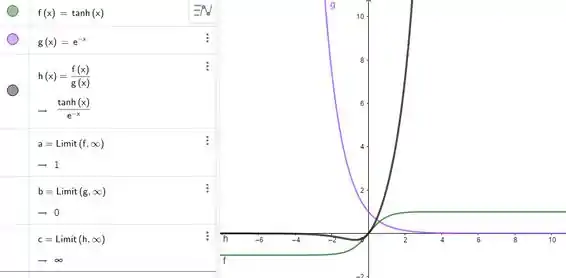
Exemplo:
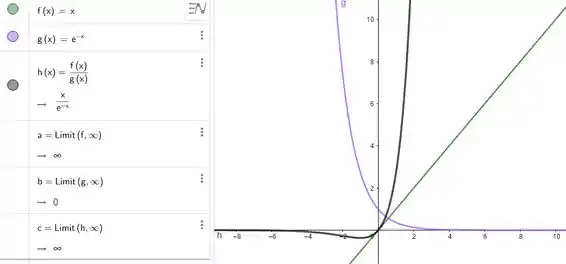
Passo 2
Verificando a letra a e a letra d
As opções a e d são bem parecidas, por isso vamos olhar elas juntas. Saca só:
- a) Teremos sempre que
- d) Teremos sempre que
As duas opção estão falando que teremos sempre alguma coisa. Já é pra ficar desconfiado de opção que impõe assim, então vamos checar elas.
Na letra , só está sendo falado de . De fato, pelo que vimos no passo anterior, existem diversos casos em que e também , como são os casos 1, 3 e 6. Mas bem, os casos 2, 4 e 5 tem e mesmo assim . Então já riscamos essa letra porque ela ta errada!
Agora, pra letra , temos algo mais errado ainda! A letra afirma a mesma coisa que a e ainda adiciona que sempre! E tem casos inclusive que mesmo que seja verdade, não é, como o caso 1 e 6. Então essa ai também a gente vai dar aquela boa riscada, porque está errada!
Passo 3
Verificando as letras b, c e e
As letras que vamos verificar agora são:
- b) Teremos sempre que
- c) Podemos ter
- e) Podemos ter
Show de bola, partiu analisar. Como em todas as letras temos produtos das funções, vamos ver como limite do produto fica em cada caso:
E olha só olha lá! Dois casos o limite do produto não dá e em nenhum caso o produto dá . Show de bola, isso elimina a opção b e e! Resta só a letra !