UnB, Sem Campus, Cálculo 2, P2 - 2008.2, Questão 5a
Sejam os vetores em e e consideremos
a) Qual a distância da origem a esta reta.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a distância da origem à reta , com e .
Pra isso, vamos considerar um ponto na origem e calcular a distância entre ele e a reta. A gente só precisa lembrar que pra isso, o ângulo que liga a reta e o ponto precisa ter um ângulo de para que essa distância seja mínima.
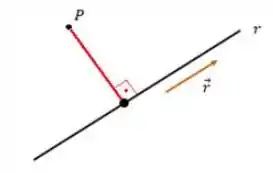
Então, pra calcular a distância entre o ponto e a reta precisamos achar um ponto na reta de modo que o vetor faça um ângulo de com o vetor diretor .
Para achar o ponto , vamos primeiro definir a reta , a partir de e , achar o vetor genérico pertencente a reta que queremos calcular a distância. Em seguida, vamos calcular o vetor , e como esse vetor deve ser ortogonal a , vamos fazer para encontrar o valor de . Encontrando , nós encontramos e conseguimos calcular a distância entre e através da fórmula da distância entre dois pontos:
Vamos lá!
Passo 2
Vamos começar definindo a reta , substituindo e :
Multiplicando o escalar pelo vetor:
Somando cada componente:
Repare que nosso vetor diretor é quem multiplica , portanto, . Vamos guardar essa informação.
Passo 3
Agora precisamos definir um ponto genérico que pertença a reta , através da equação vetorial que encontramos:
Como é um ponto na origem que definimos no passo , vamos calcular o vetor fazendo:
Passo 4
Agora vamos fazer o produto interno entre e o vetor diretor , igualando a zero:
Somando os produtos de cada componente:
Isolando :
Substituindo em , temos:
Passo 5
Agora, tendo e , podemos substituir na fórmula da distância entre dois pontos para encontrar a distância entre e a origem:
Elevando ao quadrado:
Prontinho, galera! Até a próxima! 😉