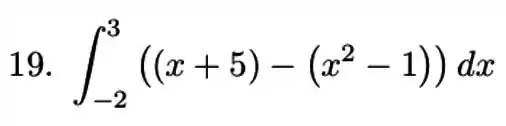Passo 1
Dá uma olhada como fica o gráfico dessas funções
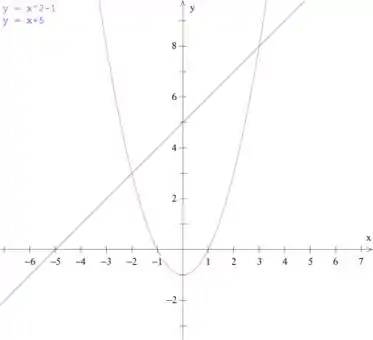
Nosso problema é encontrar a área entre essas curvas.
Passo 2
Para calcular a área da região entre essas curvas, precisamos primeiro ver os pontos de intersecção(encontro) entre elas, pra isso vamos igualar as equações.
Vamos encontrar as raízes para determinar os limites da área. Resolvendo a equação encontramos e .
Passo 3
Sabemos que para calcular uma área fazemos uma integral. Os pontos de encontro que achamos vão ser nossos limites de integração. E pelo gráfico do passo 1 vimos que nossa área está entre a curva e , então nossa integral vai ser
Passo 4
Resolvendo a integral
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x