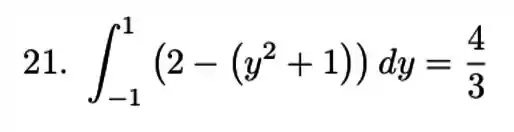Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 202123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Não precisamos fazer o gráfico para resolver, mas vamos dar uma olhada em como ele seria com a reta x = 2 e a curva x = y 2 + 1

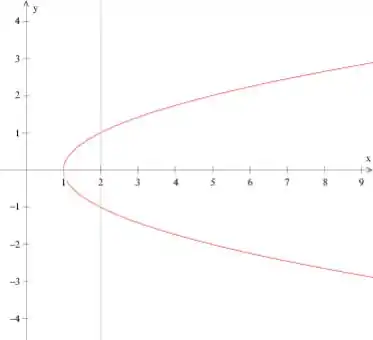
No gráfico fica melhor para visualizar a região entre a curva e a reta. Mas vamos lá resolver.

Passo 2

Pra começar precisamos encontrar as intersecções entre a curva e a reta.

2 = y 2 + 1

y 2 = 1

y = ± 1

Esses são os pontos de encontro da reta com a curva, e serão nossos limites de integração.

Passo 3

Vamos montar uma integral em y para calcular nossa área, já que assim é bem mais simples de representar nossa região. A integral vai ficar

∫ - 1 1 2 - y 2 + 1 d y

Passo 4

Integrando vai ficar

∫ - 1 1 2 - y 2 + 1 d y = ∫ - 1 1 - y 2 + 1 d y

∫ - 1 1 2 - y 2 + 1 d y = - y 3 3 + y - 1 1

∫ - 1 1 2 - y 2 + 1 d y = - 1 3 + 1 - 1 3 + 1

∫ - 1 1 2 - y 2 + 1 d y = 4 3

Essa é a área da nossa região.

Resposta

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x