UTFPR, Sem Campus, Cálculo Diferencial e Integral 3, AV2 - 2022.1, Questão 1
Calcule a área da parte do paraboloide que está abaixo do plano (adaptado)
Passo 1
Oiie, tudo certinho com você?
A questão pede para que calculemos a área do paraboloide
que está abaixo do plano . Isso significa calcular a integral de superfície relacionada a este parabolóide, ou seja
em que e são vetores obtidos através da parametrização de nosso parabolóide! Então, o primeiro passo é esse! Parametrizar o parabolóide! Vamos lá!
Passo 2
A parametrização do paraboloide é bem simples, podemos usar que
Se fizermos as derivadas parciais
Como a derivada é em relação a , temos que todos os são tomados como constante, obtendo
Da mesma forma, a derivada parcial em relação a é
Precisamos calcular o produto vetorial destes vetores para a nossa integral de superfície! Vamos fazer isso!
Passo 3
O produto vetorial é definido como
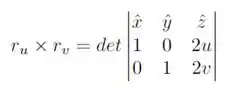
Calculando o determinante, temos que
De forma que o módulo do produto vetorial pode ser obtido como
A nossa integral de superfície pode ser escrita como
em que coloquei o em evidência e . Ainda parece meio difícil de resolver certo? Aqui o segredo está em utilizar coordenadas polares para simplificar o nosso integrando! Vamos fazer isso!
Passo 4
As coordenadas polares podem ser estabelecidas como
Nesta mudança de coordenadas, temos que devido ao jacobiano, e podemos escrever a nossa integral de superfície como
evidenciando na raiz temos que , já que . Portanto, a nossa integral se torna bastante simplificada, temos que
Mas quais são os limites de integração??? Para isso, vamos lembrar da informação de que o paraboloide está abaixo do plano . Vem comigo!
Passo 5
A intersecção entre eles nos dá a seguinte expressão
que é a equação de uma circunferência de raio . Devido ao formato do paraboloide, esta circunferência nos indica que e que . Ou seja, a nossa integração tem a forma
Como temos que e são variáveis independentes e não há nenhuma dependência indicada no integrando, ou nos limites de integração, podemos resolver as integrais separadamente, temos que
e, a integral na coordenada radial é tal que
Lembra como resolvê-la? Utilizamos substituição simples! Saca só!
Passo 6
Note que ao derivarmos a função dentro da raiz, podemos obter o que está fora, ou seja, se fizermos
e
Temos que a nossa integral se torna
Os limites podem ser obtidos como e , e identificando a primitiva temos que
Realizando a soma e avaliando os limites, temos que
Maravilha! Agora é só juntarmos ambos os resultados para obter que
ou, simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!