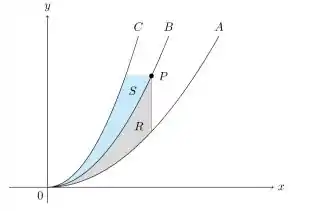
Considere as curvas , e , no primeiro quadrante do plano cartesiano, e as regiões S e R indicadas na figura abaixo. Sabe-se que para todo , a razão entre as áreas das regiões S e R é igual a 5. Quanto vale 25a?
Passo 1
E aí, galerinha! Tudo na paz por aí?
Primeiro vamos nos lembrar sobre como a gente calcula área entre curvas? Basicamente a gente faz a diferença da integral da curva superior pela curva inferior, onde os limites de integração vão ser os pontos onde elas se encontram. Nesse caso por exemplo, olhando pro desenho sabemos que um dos limites da integração é quando , e o superior é quando .
Agora que vimos isso, bora seguir!!!
Passo 2
Sabemos que a curva C está acima da B e que está acima de A, então por exemplo, se quisermos saber quanto vale a área S, temos que fazer:
O enunciado também nos diz que para qualquer ponto P pertencente à curva B, temos que a razão entre as áreas S e R é igual a 5, ou seja:
Passo 3
Isso indica pra gente que:
Pronto, problema formulado!! Agora, só temos que descobrir que diacho é esse do ponto P, correto? Note que o enunciado disse que é para QUALQUER ponto P pertencente a curva B, então isso nos indica que podemos escolher um valor arbitrário pra saber qual será o valor da curva B nesse ponto. Por exemplo, vamos escolher .
Para , temos que , ou seja, temos na curva B que para x = 1 , y vai valer 7. Ou seja, podemos delimitar esse valor nas nossas integrais.
Note que isso foi dentro do intervalo de 0 até 1.
Resolvendo pra , temos:
Logo,
Passo 4
Passo 5
Mas podemos reescrever esse sen³(x) = sen²(x)sen(x), certo?
Fazendo a distributiva, temos:
A primeira integral vai nos dar:
Passo 6
Vamos pensar no seguinte aqui pra usar de malandragem: “quem que quando eu derivo vai dar cos²(x)sen(x)?
Se você derivar esse carinha aí de cima, tu concorda que vai dar:
Mas aí apareceu um 3 multiplicando esse cara que não apareceu no nosso integrando ali, certo? Então aí vem a malandragem, quando isso acontecer, basta você dividir por esse fator que tá ali!
Em outras palavras:
E como sabemos o valor de , logo:
Passo 7
Perceba que a integral que ficou faltando resolver foi:
Que se observamos nos diz que teremos uma função de sen(x) que será integrada e vai nos conceder uma função de cos(x), que já vimsoq eu no intervalo de até nos dará zero!
Logo:
E por fim
Logo