UFF, Sem Campus, Cálculo IIA, Avaliações a Distância (AD) - AD1 - 2023.1, Questão 2d
Considere a região compreendida entre os gráficos de e , sabendo que os vértices da região considerada ocorrem em e .
Encontre a área da região .
Passo 1
Fala gente bonita, tudo na paz?
Nessa questão recebemos funções que delimitam uma região .
Além disso, o enunciado também nos informou os pontos em que ocorrem intersecções dessa curva na região , ou seja, os vértices de : .
Analisando os nossos pontos de intersecção já esboçamos a região e encontramos:
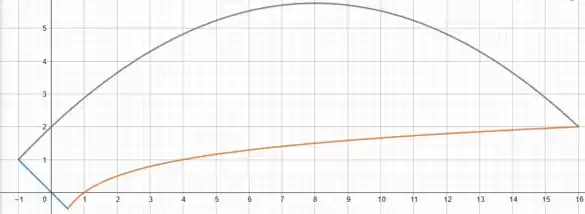
Além disso, dividindo a região em vários trechos pelos intervalos em , também encontramos a seguinte expressão para a área de :
O nosso objetivo nesse item é determinar a área de . Ou seja, em suma, vamos ter que resolver essas integrais acima.
Bora lá?! Mãos à obra!!
Passo 2
Queremos calcular a expressão:
Para isso, vamos calcular cada uma das integrais separadamente.
Começando por:
Para calculá-la devemos lembrar da regra de integração de polinômios:
Usando essa ideia, temos:
Logo, substituindo os limites de integração temos:
Perfeito!
Passo 3
Vamos agora para a segunda integral:
A maior parte do integrando é um polinômio, cujas primitivas vimos no passo anterior. Precisamos apenas saber qual a primitiva de
Olhando a tabela das integrais, temos:
Perfeito! Vamos então voltar para a nossa integral definida:
Substituindo os limites de integração:
Logo, fazendo essas continhas...
Excelente! Juntando os dois resultados temos que:
Ufaaa! Finalizamos essa questão!
Obrigado pela atenção gente, até a próxima 😊