UFF, Sem Campus, Cálculo IIA, Avaliações a Distância (AD) - AD1 - 2023.1, Questão 4a
Considere a região plana limitada pela curva , pelo eixo e pelas retas e .
Calcule a área de por uma ou mais integrais definidas em termos de .
Passo 1
Fala aí pessoal, tudo bom?
Então, nessa questão temos uma região que é limitada pelas curvas:
Precisamos calcular a área dessa região usando integrais em termos de .
Bom, para fazer isso, precisamos primeiro esboçar a região . Após fazer isso, podemos usar que a área de uma região limitada entre duas curvas, e , em um intervalo em é dada por:
Massa? Então vamo nessa!
Passo 2
Pra esboçar essa figura, vamos começar analisando as retas:
São retas verticais passando por esses pontos. Além disso, também temos uma limitação inferior no eixo . Assim, temos a seguinte região (por enquanto):
Vamos agora analisar a nossa curva:
Aplicando o logaritmo na base dos dois lados, temos:
Essa é uma clássica curva logarítmica, que tende a quando , e tende a , quando . Assim, plotando nesse mesmo gráfico:
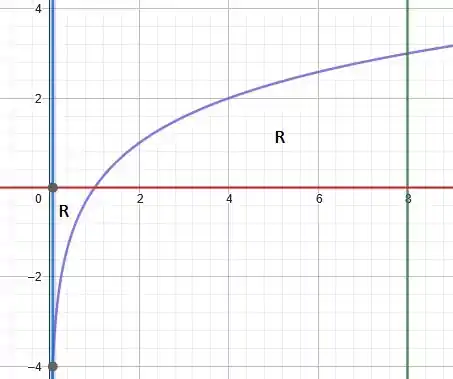
Sendo assim, temos dois trechos compondo a região : um abaixo do eixo e outro acima.
Vamos montar uma integral para cada uma dessas regiões. Para isso, precisamos calcular as intersecções da curva com as retas e .
Então, o vértice da região inferior é .
Já para o vértice da região superior, temos:
Excelente! Então, nossa região inferior está no intervalo:
E, a região superior:
Assim, como na região inferior nosso trecho está limitado entre a curva (à direita) e (à esquerda), usando a expressão do passo anterior, temos que:
Já para a área superior, o papel se inverte um pouco. Temos , à direita, e à esquerda.
Assim:
Massa!
Juntando as duas expressões, temos:
Muito bom!!
Passo 3
Vamos agora resolver essa integral!
Temos:
Lembrando que a primitiva da função , vale:
Assim, temos:
Substituindo os limites de integração:
Logo:
Prontinho gente!
Até a próxima 😊