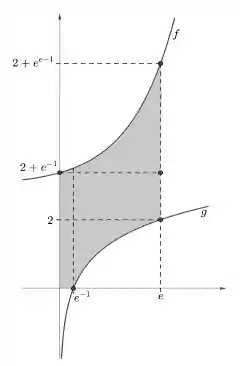
Considere a região plana
- Esboce a região
- Escreva a área da região como uma soma de duas integrais na variável . Atenção Neste item não é necessário calcular as integrais.
- Escreva a área da região como uma soma de três integrais na variável . Atenção Neste item não é necessário calcular as integrais.
- Calcule a área da região
Passo 1
Opa, vamos lá. Antes de mais nada, vamos precisar fazer um bom esboço. Afinal, ele que vai nos ajudar a calcular a área depois. Vamos ver primeiro isso aqui:
Pra função que delimita por baixo, temos:
Pra esboçar essa curva é interessante a gente lembrar que pra funções logarítmas:
Mas como também ta valendo pra , temos que considerar essa curva só a partir do eixo . E quando ela toca? Vamos ver?
Show de bola, agora pra curva que delimita por cima:
É interessante lembrarmos que das propriedades das exponenciais:
Mas como também, só vamos nos preocupar com a parte dessa curva que tá a direita do eixo . Opa, vai ser interessante então eu também anotar em que ponto que a curva toca esse eixo:
E pra fechar basta só a gente olhar para a condição . Para a curva de cima e de baixo, respectivamente, teremos o seguinte valor de para esse valor de :
Seja então:
Temos o suficiente pra esboçar! Bora lá então:
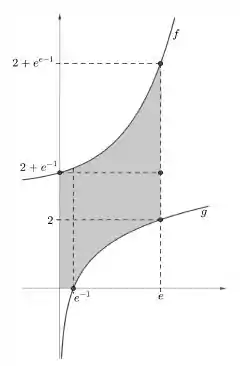
Passo 2
Agora vamo olhar presse zinho ae e tentar modelar uma fórmula pra área em função de . Como a integral é a área abaixo de uma curva, se quiséssemos calcular a seguinte área:
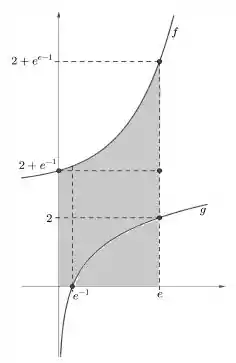
Era só fazer a integral da curva de cima usando as delimitações de como limite de integração! Ficaria:
Ok, mas isso não é exatamente né? Calma gafanhoto, chegaremos lá. Agora imagina que eu quero calcular essa área:
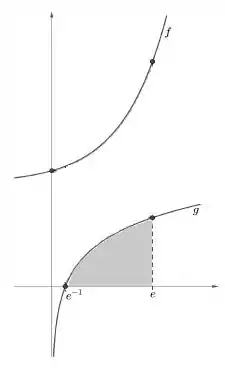
Mesma ideia! Só que agora só precisamos nos preocupar com a curva de baixo. Nota no entanto que os limites de integração vão ser diferentes, então muito cuidado ai! Vamos ter:
E como a área da região pode ser entendida como a primeira área calculada aqui menos a outra, temos:
Passo 3
Beleeeza, agora vamos fazr a mesma coisa, só que em termos de . Note que as duas curvas podem ser invertidas. Pra de baixo:
E pra de cima:
Pra entender as curvas e , é só pensar que elas são exatamente como se pegássemos as curvas originais e fizéssemos essas operações:
![]()
Nesse caso, teríamos (agora com eixo horizontal e vertical ):
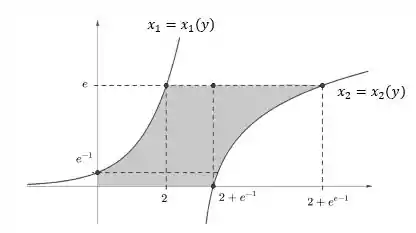
Show de bola, só precisamos agora modelar as integrais da mesma forma que fizemos da outra vez. Pra começar, olha essa região aqui:
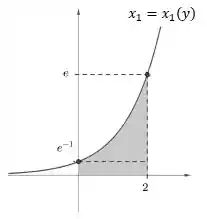
Esse aqui pra calcular é bem direto ao ponto, viu? Afinal, é a área abaixo do gráfico da curva . Logo:
Show, próxima área. Dá uma olhada nessa aqui:
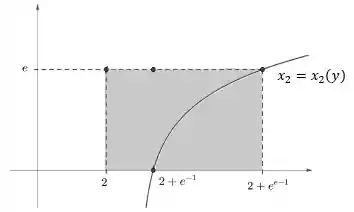
Essa aí é de boas! É a área de um retângulo ou então, em linguagem de cálculo, a integral abaixo do gráfico de uma função constante de valor . Essa área é representada por:
Bem, se a gente somasse as duas primeiras áreas, teríamos a seguinte região:
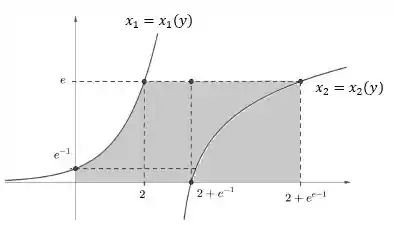
Mas nã é bem isso que queremos né? Não exatamente. Afinal, o pedacinho abaixo...
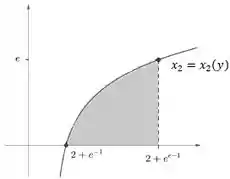
...a gente não está contando! Então além de somar as duas anteriores, vamos ter que subtrair essa! Como essa é a área abaixo da curva , vamos ter:
E tai! Fechamos! A área no final das contas vai ser:
Passo 4
Ufa, última parte! Agora é calcular a área. Como a gente já tem a fórmula montada e podemos escolher, bora então escolher a mais simples, que tem menos integrais! Seja:
Para a primeira integral, como
Para a segunda, temos que considerar uma integração por partes para o termo de . Seja e , pela integração por partes:
Sendo assim, nossa outra integral será:
Somando finalmente os resultados, partimos pro abraço!