Deseja-se calcular a área sob o gráfico da função para
- Explique, por meio de um teorema, por que utilizamos uma primitiva da função para o cálculo da área sob seu gráfico.
- Utilize a substituição e reescreva a integral apenas em termos da variável .
- Utilize a substituição e reescreva a integral apenas em termos da variável .
- Escolha um dos itens acima para determinar a área desejada.
Passo 1
Vamos começar entendendo o seguinte, quando queremos calcular a área abaixo de uma curva dada por uma função podemos pensar nessa figura aqui:
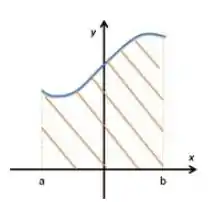
Pelo Teorema Fundamental do Cálculo, entramos o conceito da Primitiva de uma função , nós temos a relação:
Logo, quando integramos a função dentro de um limite de integração, encontraremos a primitiva do maior valor menos a primitiva do menor valor de integração:
Então essa diferença entre as primitivas aplicadas nos pontos máximo e mínimo define a área abaixo da função!
Passo 2
A letra “b” já é mais prática, ela nos pede para realizar a substituição:
E reescrever a integral apenas em termos da variável . Então, relembrando, nossa função é:
Então queremos achar a integral:
Se já sabemos quem é , temos que encontrar :
Derivando os dois lados, ficamos com:
Então:
Porque escolhemos fazer desse jeito? Porque temos dentro da integral!
Vamos colocar isso na nossa integral:
Um ponto que temos que dar muita importância são os limites de integração, já que estamos passando tudo de para , temos que recalcular os limites de integração:
Então, quando :
Enquanto, quando :
Então os novos limites são:
Como temos um sinal dentro de subtração dentro da integral, podemos inverter os limites da integral:
Não precisa resolver, porque a questão só nos pediu para reescrever a integral!
Passo 3
A letra “c” nos pede outra substituição, dessa vez:
E vamos reescrever para ter apenas !
Nossa integral já é conhecida:
Vamos começar calculando quem é , derivando os dois lados de:
Encontramos:
Então vamos substituir isso tudo na nossa integral:
Vamos melhorar isso aqui:
Colocando o em evidência:
Como sabemos da relação:
Então:
Substituindo:
Então a única coisa que falta fazer é definir os limites de integração:
Então para encontrar , temos que fazer:
Quando , então:
Quando , então:
Logo, nossa integral se torna:
Terminamos nosso problema!
Passo 4
A letra “d” nos pede para escolher uma das duas integrais para resolver, nesse caso, eu acho mais fácil da gente resolver a letra “b”:
Vamos colocar a constante para fora da integral:
Vamos finalizar:
Acabou geral! Nos vemos no próximo exercício!
Resposta
- Demonstração