- Determine a área da região delimitada pelas curvas e
Passo 1
Pow, nesse tipo de exercício, ajuda muito se antes a gente entender quem é a região, e como essas duas curvas se relaciona.
Bem, podemos identificar que a primeira curva é aquela reta passando pela origem
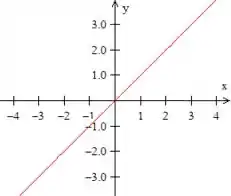
Quanto a curva é uma parábola que passa pela origem e o ponto quando se anula
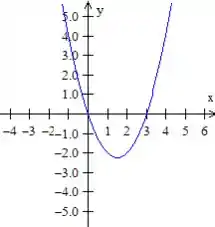
A junção dessas duas curvas terá a região amarela
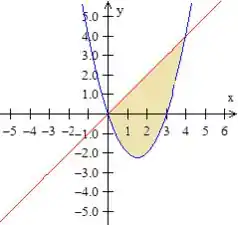
Passo 2
Bem, acabamos de ver a interação das duas curvas no desenho formando a região que queremos a área.
Mas como podemos descobrir quem são aqueles pontos que as duas se encontram?
Pra responder essa pergunta, olharemos para a interação dessas duas curvas, mas agora uma interação matemática, ou seja
resolver esse sistema com as duas curvas!
Substituindo o de cima na de baixo
colocando o em evidência...
logo, ou ou
Logo, os dois pontos são como poderíamos imaginar pelo gráfico o e o
Passo 3
Bem, agora que a gente conhece bem a região que estamos trabalhando, podemos calcular a área, lembrando-se da fórmula:
Onde esses termos e aí é o limite mínimo e máximo de que no nosso caso acabamos de ver que é e
Lembrando que pela teoria a é a função que está por cima e a , a que está por baixo, ou seja
portanto
Passo 4
Agora é só calcular essa integral aí e correr para o abraço
Integrando esse polinômio
Substituindo esses limites...