- Determine os valores de para os quais
- Sejam e os valores encontrados no item , determine a equação da parábola que tem vértice em e cujos pontos de interseção com o eixo são e
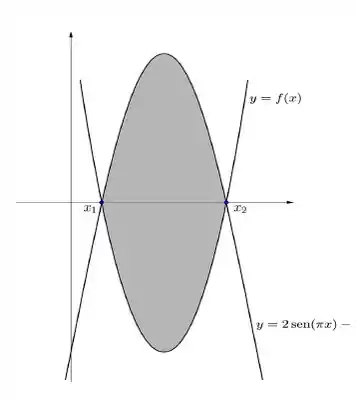
- Esboce a região abaixo onde é a função determinada no item e e são os valores encontrados no item
- Calcule a área da região
Passo 1
Partiu começar. Bem, a primeira coisa que a gente pode notar é que se:
Então se eu multiplicar por , eu posso multiplicar o intervalo também:
Opa, se o argumento do , que é , ta dentro desse intervalo, sabemos que o arco necessariamente está dentro de uma volta do círculo tirgonométrico! Manipulando a equação:
Agora a gente precisa achar o arco cujo seno é e esse arco tem que pertencer ao intervalo . Oras, esse não é um daqueles valores clássicos de seno? Olha só a tabela abaixo com alguns valores diretos:
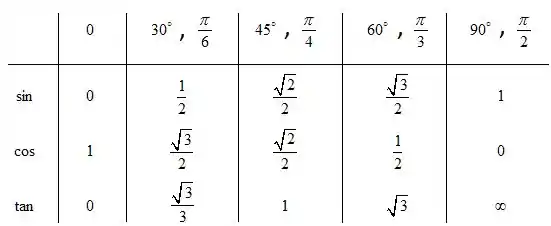
Pelo que vimos então o arco cujo seno é é graus ou e logo:
Mas antes de fecharmos essa letra, temos que lembrar uma propriedade importantíssima:
Em outras palavras:
Se o arco possui o mesmo seno que o arco então não só será válido
Como vimos, mas também será válido:
E logo, pode assumir outro valor! Fechamos essa letra. Vamos ter:
Passo 2
Pra letra a gente pode pensar numa parte importante do enunciado: “cujos pontos de interseção com o eixo são e ”. Galera, ponto de interseção com o eixo e raízes são a mesma coisa! Sendo assim, podemos escrever a equação da parábola segundo o modelo:
E como conhecemos:
Vamos ter:
Show de bola. Pra gente fechar falta só achar que é o nessa equação. Pô, o enunciado deu pra gente o ponto que faz parte da curva! Então se substituirmos as coordenadas desse ponto na equação...:
E logo:
A equação final da parábola será:
Passo 3
Vamos esboçar agora:
Pra começar, nota o seguinte, verticalmente, está limitado por e . Então se a gente chamar esse carinha de :
Como na letra achamos os valores de que satisfaziam:
Achamos então as raízes de ! Afinal isso é o mesmo que achar tal que:
E olha só! Essas raízes são as mesmas de e são exatamente os valores de que delimitam a região . Sendo então:
- Uma parábola uma função com “cara de copo”, com a boca virada pra cima já que
- Uma função seno uma função oscilatória que no intervalo está acima do eixo , uma vez que só a partir do arco que o seno inverte de sinal.
Um bom esboço que podemos fazer é:
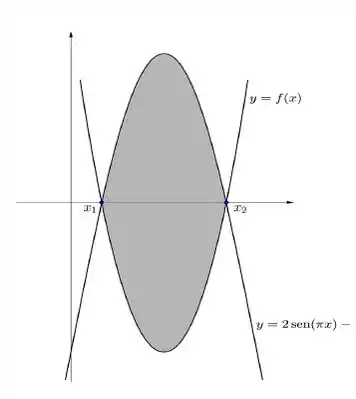
Passo 4
Calma galera, ta acabando. Falta só achar a área dessa região doida que esboçamos, pra isso, podemos dividir ela em duas:
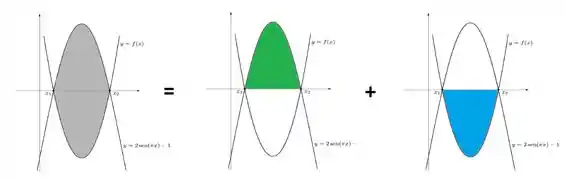
Calculando primeiro a área verde, como a função que ta acima do eixo é a senoidal, e também já sabemos os limites de integração, montamos de boas essa área:
Como, do círculo trigonométrico:
Vamos ter:
Substituindo na equação da área:
Da tabelinha no passo tiramos:
Agora pra área azul, vamos ter:
Como essa integral é uma integral só de polinômios, resolvemos ela de forma direta viu? Vamos ter:
Colocando tudo no mesmo denominador
E daqui em diante é só conta e mais conta pra ter certeza que fizemos tudo certinho
Somando as duas áreas, vamos ter: