Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 281123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Área entre Curvas

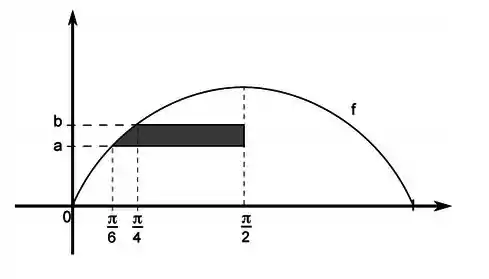
Na figura abaixo, sabendo que f x = s e n x , determine os valores de a e b e calcule a área da região destacada.

Passo 1

Sabemos que, pelo gráfico:

a = f π 6

Portanto:

a = s e n π 6

a = 1 2

Analogamente, temos:

b = s e n π 4

b = 2 2

Passo 2

Entre x = π 4 e x = π 2 temos apenas um retângulo, de área:

A = b a s e × a l t u r a

A = π 2 - π 4 × b - a

A = π 2 2 2 - 1 2

A = π 4 2 - 1

Passo 3

De resto, precisamos fazer a integral da área debaixo da função f menos o retângulo cuja altura é a . Podemos escrever da seguinte maneira:

A ' = ∫ π 6 π 4 f x - a d x

Calculando:

A ' = ∫ π 6 π 4 s e n x - a d x

A ' = - cos ⁡ x - a x π 6 π 4

A ' = - cos ⁡ π 4 - cos ⁡ π 6 + a π 1 4 - 1 6

A ' = - 2 2 - 3 2 + a π 12

A ' = 1 2 2 - 3 - a π 6

Passo 4

Pondo tudo de volta:

A r e a = 1 2 2 - 3 - a π 6 + π 4 2 - 1

Arrumamos, de forma que:

A r e a = 1 2 2 - 3 + π 2 2 - 1 - a 3

Dependendo de como você arrumar, pode achar algo um pouco diferente...

Resposta

1 2 2 - 3 + π 2 2 - 1 - a 3

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x