Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 261123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Prova Cálculo B MAT1158 P1

Seja R a região plana dada por

R = { x , y ∈ R 2 | x ≥ 2 y - 1 2 ,   y ≥ x - 2 ,   y ≤ 4 - x }

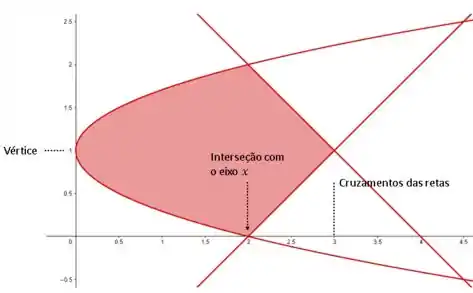
  1. Esboçe abaixo a Região R . Indique explicitamente em seu desenho as coordenadas dos seguintes pontos:

  • Vértice da parábola
  • Ponto de interseção da parábola com o eixo x
  • Ponto de interseção entre as duas retas
  • Escreva a área da região R através de uma soma de duas integrais na variável x

    • Atenção: Neste item não é necessário calcular as integrais

  • Escreva a área da região R através de uma soma de duas integrais na variável y

    • Atenção: Neste item não é necessário calcular as integrais

  • Calcule a área da região R utilizando o método que preferir

    • Passo 1

    Vamos analisar nosso conjunto e assim conseguir plotar a nossa região.

    A primeira função que temos é x ≥ 2 y - 1 2

    Tome o caso mais geral da nossa inequação dado por

    x ≥ a y ± b 2

    Na qual a indica a inclinação da nossa curva e b o deslocamento que ela tem em relação a origem. O sinal ± sugere para que lado estamos caminhando. Quando temos o sinal positivo, estamos indo sentido ao lado negativo em nosso gráfico, e quando o sinal é negativo estamos caminhando para o lado positivo.

    Assim tomando a equação

    x = 2 y - 1 2

    É uma parábola, só que deitada e relação ao que estamos acostumados. O sinal de a = + 2 indica que ela cresce no sentido positivo de x . Além disso ela está deslocada para cima no eixo y .

    As outras duas inequações se referem a duas retas. Agora podemos começar a desenvolver nosso problema e determinar o que é pedido

    Passo 2

    O vértice da parábola já foi dado no passo 1, percebeu? Como olhando para nossa função x = 2 y - 1 2 , já conseguimos determinar que ele se encontra em 0,1 .

    Agora os pontos de interseção da parábola com o eixo x , basta tomar

    x = 2 0 - 1 2

    Que implica

    x = 2

    E agora a interseção entre as duas retas

    y = x - 2 y = 4 - x

    Assim temos que

    x - 2 = 4 - x → 2 x = 6 → x = 3 → y = 1

    Que é onde nossas retas se cruzam. Assim temos

    Passo 3

    (b) Então supondo querer achar a área da nossa superfície. Logo teriamosque dazer então

    A = ∬ d y d x = ∫ 0 2 ∫ y 1 y 2 d y d x + ∫ 2 3 ∫ y 3 y 4 d y d x  

    Mas quem são nossos y i ?

    No intervalo x ∈ 0,2 , temos que y ∈ 1 - x 2 , 1 + x 2 . E no intervalo x ∈ 2,3 nosso y   i n   [ x - 2,4 - x ]

    Assim nossa área pode ser escrita como

    A = ∫ 0 2 y 2 - y 1 d x + ∫ 2 3 y 4 - y 3 d x

    = ∫ 0 2 1 + x 2 - 1 - x 2 d x + ∫ 2 3 4 - x - x - 2   d x

    Passo 4

    (c) Agora queremos fazer invertendo os limites de integração, assim temos

    A = ∫ 0 1 ∫ x 1 x 2 d x   d y + ∫ 1 2 ∫ x 3 x 4 d x   d y

    E agora precisamos determinar quem é x i

    Sabemos que quando y ∈ 0,1 implica que x ∈ [ 2 y - 1 2 , 2 + y ] e em y ∈ 1,2 temos que

    x ∈ [ 2 y - 1 2 , 4 - y ] .

    Assim temos que

    A = ∫ 0 1 x 2 - x 1 d y + ∫ 1 2 x 4 - x 3 d y

    = ∫ 0 1 2 + y - 2 y - 1 2   d y + ∫ 1 2 4 - y - 2 y - 1 2   d y

    Passo 5

    (d) Agora só precisamos calcular nossa área. Vamos calcular pelo segundo método?

    A = ∫ 0 1 2 + y - 2 y - 1 2   d y + ∫ 1 2 4 - y - 2 y - 1 2   d y

    A = ∫ 0 1 [ - 2 y 2 + 4 y - 2 + 2 + y ] d y + ∫ 1 2 [ - 2 y 2 + 4 y - 2 + 4 - y ] d y

    A = ∫ 0 1 [ - 2 y 2 + 5 y ] d y + ∫ 1 2 [ - 2 y 2 + 3 y + 2 ] d y

    E agora integrando

    A = - 2 y 3 3 + 5 y 2 2 0 1 + - 2 y 3 3 + 3 y 2 2 + 2 y 1 2

    A = - 2 3 + 5 2 + - 16 3 + 6 + 4 - - 2 3 + 3 2 + 2

    A = 15 - 32 + 36 + 24 - 9 - 12 6 = 22 6 = 11 3

    Resposta

    1. Vértice ( 0,1 ) , interseção eixo x x = 2 , interseção entre retas 3,1
    2. A = ∫ 0 2 1 + x 2 - 1 - x 2 d x + ∫ 2 3 4 - x - x - 2   d x
    3. A = ∫ 0 1 2 + y - 2 y - 1 2   d y + ∫ 1 2 4 - y - 2 y - 1 2   d y
    4. A = 11 / 3

    Exercícios de Livros Relacionados

    Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
    Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
    Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x