Seja a região plana dada pelo esboço abaixo:
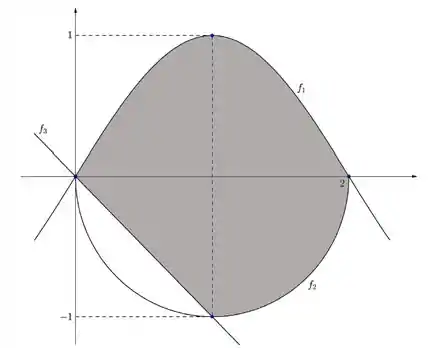
Onde ,e são funções tais que:
- , com uma constante
- O gráfico de é uma semicircunferência com máximo nos pontos e
- O gráfico de é uma reta que passa pela origem e pelo ponto de mínimo da função
- Determine a expressão das funções ,e
- Escreva a área da região como uma soma de duas integrais na variável
- Calcule a área da região
Passo 1
Gráfico de
Vamo que vamo. A questão tá pedindo a expressão das funções na letra . Beleza, vamos começar com . Já sabemos que:
Precisamos achar então . Ok, ok, mas e agora? Bem, vamos olhar com calma pro círculo trigonométrico:
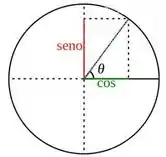
Po, essa função só zera quando o ângulo é igual à 0 ou um múltiplo inteiro de ! Sendo assim
Mas pelo gráfico, vemos que:
Onde o primeiro resultado é o equivalente à e o segundo à . Se então:
E pronto, achamos o . Agora só escrever na função:
Passo 2
Gráfico de
Beleza, temos uma semicircunferência em mãos e queremos uma expressão pra . Pra começar a resolver esse cara aqui, vamos lembrar que a equação de uma circunferência é:
Onde é o ponto do centro da circunferência e é o raio dela. Pelo gráfico, vemos que:
Sendo assim, a equação fica:
Rearranjando, temos:
Como queremos só a parte de baixo da circunferência, vamos desconsiderar o sinal positivo, beleza? Fechamos então nossa equação da semicircunferência como:
Passo 3
Gráfico de
Pra fechar a letra falta só a , que vai ser nada mais nada menos que uma reta. Oras, retas também tem uma cara específica. A função vai ser então algo assim:
Falta a gente achar e . Pra isso, vamos ver os pontos em que a reta passa no gráfico:
Opa, se passa pela origem, então:
E no segundo ponto vamos ter:
Show! Fechamos a última equação. A reta vai ser então:
Passo 4
Escrever a área da região
Vamos falar de áreas agora então. A primeira coisa a se fazer é dividir a região em 4 regiões menores:
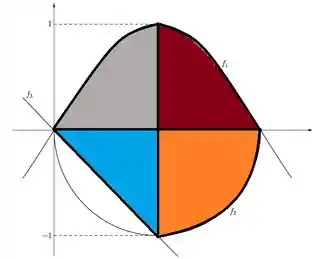
Agora, a gente tem que lembrar uma coisa muito importante: Não existem áreas negativas. Então se calcularmos as integrais das regiões azul e laranja, o resultado vai dar negativo! Pra gente não errar ai, vai ser importante então a gente adicionar um sinal de negativo pra essas áreas.
Então vamos lá. Pra área cinza e vermelha, temos a integral de , que já dá uma área positiva! As áreas vão ser:
Pra área azul, temos uma integral de , que daria uma área negativa. Então vamos ter:
E pra área laranja, temos uma integral de , que também daria uma área negativa. Aplicando a mesma ideia, temos:
Mas perai, temos 4 integrais, a questão quer a área como soma de duas integrais! Não seja por isso! Veja que a área cinza e a azul tem os mesmos limites de integração! Então podemos fazer assim ó:
E pra área vermelha e laranja a ideia é a mesma. Vamos ter então:
Como a região é a soma de todas as cores, temos:
Passo 5
Calcular a área da região
Vamos calcular a área. Pra calcular, a gente poderia só realizar a integral do passo anterior, mas olha só com o que a gente teria que lidar:
Não é lá uma integral muito bonita né? Pra facilitar, vamos usar a geometria, belê? Olha só:
Sendo assim, calculamos essas áreas através das fórmulas
Como a base do triângulo, a altura do triângulo e o raio da circunferência são coincidentemente iguais a , temos que as áreas vão ser:
Agora falta calcular a área da região cinza e da vermelha. Essa não tem jeito, vai ter que ser via integral mesmo. Do passo anterior, temos:
Sendo assim:
Calculamos então:
Somando todos os resultados, temos: