Sejam as raízes da função .
Seja a função quadrática cujo gráfico passa pelo ponto e que possui raízes e .
Seja a região delimitada pelos gráficos de e .
a) Determine a expressão da função .
b) Determine o crescimento e o decrescimento de .
c) Faça abaixo um esboço da região . Indique explicitamente em seu desenho as coordenadas (abscissas e ordenadas) de todos os pontos de intersecção entre os gráficos de e .
d) Escreva a área de como uma soma de duas integrais na variável .
Passo 1
a) Antes de qualquer coisa, vamos achar as raízes da função , porque tendo e , conseguimos encontrar :P
A primeira raíz, de cara, é .
Resolvendo , temos:
Então, as 3 raízes de são .
Como , vamos organizar em ordem crescente:
Passo 2
Então as raízes da função , ou seja, onde essa função cruza o eixo , são em e em .
Podemos escrever uma função quadrática de forma fatorada:
Onde e são nossas raízes e e vai definir se nossa parábola vai estar pra cima ou pra baixo. Então
Substituindo o ponto , para encontrarmos :
Então:
Passo 3
b) Para estudarmos crescimento e decrescimento de uma função, precisamos estudar o sinal da sua primeira derivada, certo?
Vamos encontrar as raízes de
Então os pontos e são os pontos críticos da nossa função, ou seja, onde ela irá mudar seu crescimento/decrescimento.
Vamos analisar quando ela cresce e quando decresce.
Passo 4
Temos os seguintes intervalos para analisar o sinal de :
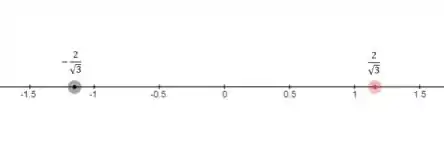
Como tem a concavidade pra cima (pois ), temos:
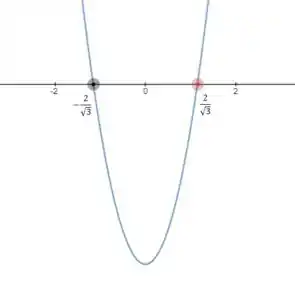
Onde a parábola estiver acima do eixo, nossa é positiva, e onde estiver abaixo, é negativa, ou seja:

Logo:
Os intervalos de crescimento de são .
O intervalo de decrescimento de é .
Passo 5
c) Primeiro vamos encontrar os pontos de intersecção de e , igualando as duas funções:
Temos de cara a solução , e aí resolvendo
Então, as intersecções das funções são nos pontos
Abaixo temos o esboço dos gráficos das funções (em verde) e (em roxo) com a região e os pontos de intersecções marcados:
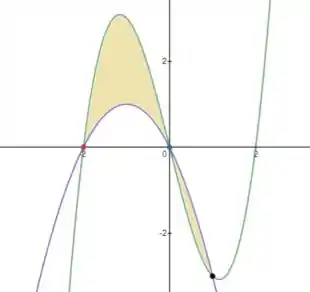
Passo 6
d) A área de é a área de entre e e entre e :
Passo 7
e) Vamos calcular a integral do item anterior:
Resolvendo as integrais:
Então, a área de é
Resposta
a)
b) Os intervalos de crescimento de são .
O intervalo de decrescimento de é .
c)
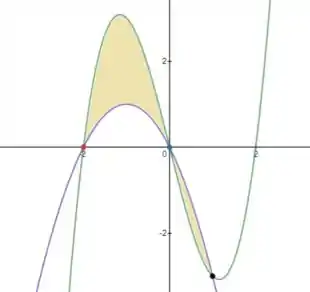
d)
e)