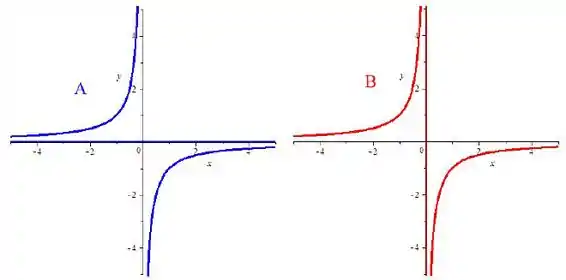
Considere a função
Desenhe as curvas contidas no conjunto
E no conjunto
Apontando no desenho o conjunto e o conjunto .
Passo 1
Para desenhar essas curvas, precisamos primeiro saber quem são as derivadas parciais, certo?
Então vamos lá.
Pela regra do produto e da cadeia:
Passo 2
Show, agora que já temos as derivadas parciais, vamos descobrir quem são as curvas contidas em cada conjunto. Começando pelo conjunto ., fazemos
Para que isso seja verdade,
Ou
Porque independente dos valores de e .
Passo 3
Assim, temos que corresponde ao eixo e corresponde a uma hipérbole.
Nosso desenho fica então:
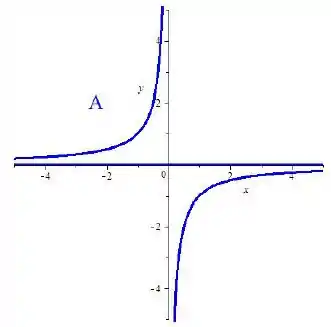
Passo 4
Agora vamos ver o que acontece no conjunto . Fazemos
Isso só é verdade se
Ou
Porque independente dos valores de e .
Passo 5
Assim, nosso desenho fica muiiito parecido com o desenho do conjunto . A única diferença é que corresponde ao eixo .
Temos então
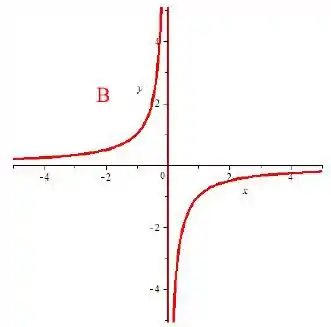
Resposta