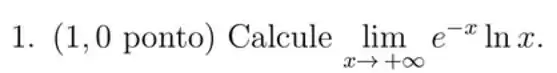
Passo 1
Substituindo:
Vimos que vamos ter uma indeterminação de .
Passo 2
Para fugir dessa indeterminação, vamos transformá-la num quociente e então aplicar a Regra de L’Hospital para resolvê-lo:
Usando L’Hospital:
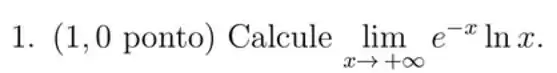
Substituindo:
Vimos que vamos ter uma indeterminação de .
Para fugir dessa indeterminação, vamos transformá-la num quociente e então aplicar a Regra de L’Hospital para resolvê-lo:
Usando L’Hospital: