Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra de L’Hospital – Outras Indeterminações

Ver Teoria
Exercício 100123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899

Enunciado

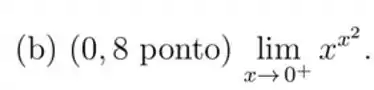
Passo 1

Pra esse limite, vamos usar a propriedade da exponencial com o log:

f x = e ln ⁡ f x

lim x → 0 + ⁡ x x 2 = lim x → 0 + ⁡ e ln ⁡ x x 2

Temos a propriedade do log de uma exponencial, de onde fica:

lim x → 0 + ⁡ e ln ⁡ x x 2 = lim x → 0 + ⁡ e x 2 ( ln ⁡ x ) = e lim x → 0 + ⁡ x 2 ln ⁡ x

Vamos focar no limite do expoente:

lim x → 0 + ⁡ x 2 ln ⁡ x

Passo 2

Nesse limite, substituindo temos uma indeterminação:

lim x → 0 + ⁡ x 2 ln ⁡ x = 0 2 ln ⁡ 0 + = 0 - ∞

Vamos transformar essa indeterminação em um quociente e aplicar L’Hospital:

lim x → 0 + ⁡ x 2 ln ⁡ x = lim x → 0 + ⁡ ln ⁡ x 1 x 2 = lim x → 0 + ⁡ ln ⁡ x x - 2

lim x → 0 + ⁡ ln ⁡ x x - 2 → L ' H lim x → 0 + ⁡ ln ⁡ x ' x - 2 ' = lim x → 0 + ⁡ 1 x - 2 1 x 3

= lim x → 0 + ⁡ x 2 - 2 = 0 2 - 2 = 0

Passo 3

Logo, o resultado será

lim x → 0 + ⁡ x x 2 = lim x → 0 + ⁡ e ln ⁡ x x 2 = e lim x → 0 + ⁡ x 2 ln ⁡ x = e 0 = 1

lim x → 0 + ⁡ x x 2 = 1

Resposta

lim x → 0 + ⁡ x x 2 = 1

Exercícios de Livros Relacionados

Use a regra de L’Hopital para determinar o seguinte exercício: l i m x → ∞ x 1 / l nx
Determine o limite:underset(x - 0^+)(lim) (1 + (1)/(x))^x
Determine o limite:underset(x - oo)(lim) ((x^2 + 1)/(x + 2))^((1)/(x))
Use a regra de L’Hopital para determinar o seguinte exercício: l i m x → 0 + x 2 l nx
Encontre o limite. Use a regra de L’Hôspital quando for apropriado. Se houver um método mais elementar, considere utilizá-lo. Se a regra de L’Hôspital não se aplicar, o porquê. l i m x → 0 x x - 1 ln