UFRJ, Cálc.1, Listas do AVA, lista 17, 10
A base de é uma região elíptica delimitada pela curva . As secções transversais perpendiculares ao eixo são triângulos isósceles retos com hipotenusa na base
Passo 1
Faaalaa, beleza?? Bora para o último probleminha dessa prova.
Bom, para começar vamos lembrar como iremos calcular esse volume, para entender quais passos temos que tomar. Vamos usar que:
A ideia aqui será que o volume do sólido é dado pelos infinitos triângulos isósceles que tem suas hipotenusas perpendiculares ao eixo , varrendo a elipse. Ou seja, a é referente a esses triângulos, vamos tomar triângulos da forma:
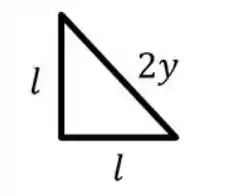
Sabemos que
Passo 2
Agora vamos pensar no seguinte. Nós temos que integrar sobre , ou seja, temos que relacionar essa área acima com , como faremos isso?
A ideia aqui será, primeiramente, relacionar com e depois usar a equaçãozinha da elipse para relacionar com , bora lá:
Por Pitágoras no triângulo, temos que:
Agora, olhando para equação
Substituindo o valor achado:
Passo 3
Agora, temos quase tudo que precisamos, bora calcular o volume:
Colocando o valor achado
Ou seja
Agora vamos analisar os limites de integração, veja que a elipse é do tipo:
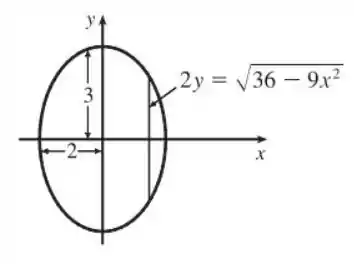
Veja que varia de para , ou seja, queremos:
Colocando em evidência dentro:
Ou seja, temos:
Resultando em:
Temos então que:
Ou seja:
Assim terminamos com a nossa listinha