UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 2ª Lista, Questão 8
Nos exercícios 05 a 12, calcule o volume do sólido descrito em cada caso, usando integração tripla.
Sólido interseção dos paraboloides e .
Passo 1
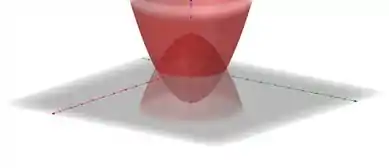
Olá amigo, Yuri aqui e na imagem acima vemos o nosso querido solido que iremos calcular o volume. Para isso iremos utilizar da integração tripla. O nosso solido está limitado inferiormente e superiormente por dois paraboloides.
Passo 2
Para facilitar nossas queridas vidas, vamos então passar de coordenadas cartesianas para coordenadas cilíndricas
Para
Já para
Então
O ângulo é
Pois damos uma volta completa aqui.
Agora falta saber que é r, igualando as duas paraboloides
Mas como um raio não pode ser negativo,
Agora é montar nossa integral
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d