Dados os gráficos de , e as 5 regiões A1,A2,A3,A4 e A5, delimitadas de acordo com a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado
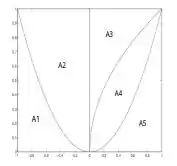
(a)A5 ao redor da reta x = 1 .
Passo 1
Eaew, belezinha?
O enunciado nos pede para formularmos a integral que calcula o volume obtido ao girar a área A5 ao redor do eixo x=1.
Para montarmos essa integral, vamos utilizar o método das cascas que obtém o volume dos sólidos de revolução. Vamos utilizar esse método, pois os retângulos de largura infinitesimal escolhidos são paralelos ao eixo de rotação, gerando cascas quando são rotacionados. Então vamos lá!
Passo 2
Primeiro vamos olhar para a área que será rotacionada, que é delimitada pelo eixo y=0 e , sendo :
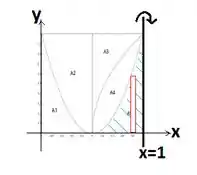
Como já dito, os retângulos são paralelos ao eixo de rotação, então é conveniente utilizar o método das cascas, sendo o elemento de volume da casca de largura infinitesimal () dado por:
Temos que é a distância do retângulo do eixo de rotação e a sua altura. Analisando a imagem, temos que:
Agora já conseguimos formular a integral para calcular o volume.
Passo 3
Montando a integral sabendo que :
Essa é a integral que calcula o volume do sólido obtido ao girar a área A5 ao redor do eixo x=1.
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta