UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Prof° Edison Figueiredo - 1ª Lista, Questão 29
Calcule o volume do sólido do primeiro octante, limitado pelas superfícies , , , , e .
(Sugestão: Faça e )
Passo 1
Oiie, tudo bem?
O sólido é formado pelas superfícies
, , , , e
Temos que a tampa deste sólido é dada por
os planos e , e as superfícies e definem as laterais. Precisamos escrever o volume da seguinte maneira
A região pode ser visualizada como
Vamos tentar obter os limites de integração! Bora lá!
Passo 2
A sugestão do enunciado é que usemos a substituição
e
para reescrever a integral precisamos calcular o jacobiano da transformação usando a definição
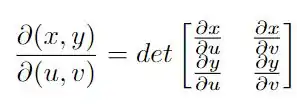
Note que se multiplicar as duas equações em , temos que
e, se dividirmos as duas equações, temos que
Sendo assim, aplicando a definição de jacobiano, podemos obter
De forma que a integral se torna
como temos que , temos que
ou simplesmente
Vamos achar os limites de integração!
Passo 3
Usando a nossa transformação de coordenadas, temos que
e
nos levam aos limites
e
e, as superfícies
e
nos levam à
e
que é uma região retangular! A nossa integral se torna simplesmente
distribuindo os produtos temos que
Como a região é retangular (limites constantes) podemos simplesmente integrar em qualquer ordem! Vamos começar com as integrais em
Passo 4
Integrando em podemos usar que
e, também
O volume se torna
Resolvendo agora a integral em , temos que
ou simplesmente
Juntando todos os resultados temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!