UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Lista de Exercícios 2, Questão 9a
Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas.
a) , , , ; em torno do eixo .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume de rotação da região definida pelas retas , , , ; em torno do eixo .
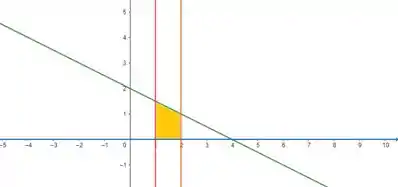
Sendo assim, nossa região em amarelo vai rotacionar em torno da reta em azul, que é o eixo .
Pelo método dos discos, nós podemos calcular o volume dos sólidos obtidos pela rotação em torno de um eixo através da equação:
No nosso caso, e o intervalo é dado pelas retas e . Então, vamos substituir essas informações e calcular a integral para obter o volume de rotação.
Vamos lá!
Passo 2
Montando nossa integral, temos:
A gente pode separar a integral da soma na soma de integrais, assim:
Integrando cada termo usando a regra da potência (), temos:
Aplicando os intervalos de integração:
Prontinho, galera! Até a próxima! 😉