UFSC, Joinville, Cálculo II, Provas Profº Rómulo Castillo - P2 2015.2, Questão 2d
Dados os gráficos de , e as 5 regiões A1,A2,A3,A4 e A5, delimitadas de acordo com a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado
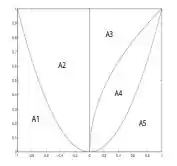
(d) Formule uma integral que calcula a área A4 usando equações paramétricas.
Passo 1
Eaew, belezinha?
O enunciado nos pede para formularmos a integral que calcula a área A4 usando equações paramétricas. Para montarmos essa integral, vamos parametrizar as curvas que delimitam essa área e utilizar a definição:
Então vamos lá!
Passo 2
Primeiro vamos olhar para a área que deve ser calculada, essa é delimitada superiormente por e inferiormente por no intervalo :
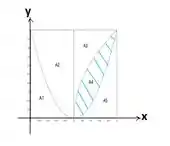
Passo 3
Parametrizando as curvas:
, sendo
, sendo
Agora já podemos montar a integral que irá calcular a área A4.
Passo 4
A área é dada por:
Note que fazemos a diferença entre a função que delimita superiormente e a que delimita inferiormente a área A4. Então a integral é
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta