Considere a região delimitada pela curva e pelas retas e :
Esboce a região .
Determine o volume do sólido obtido pela rotação da região ao redor da reta .
Passo 1
Para saber o esboço das figuras precisamos conhecer todas as curvas e seus pontos de encontro. O gráfico de uma função logarítmica é conhecido, é um gráfico que temos que saber de cabeça. Já as retas e sabemos que são retas paralelas aos eixos principais (a primeira é paralela ao eixo passando em e a segunda é o próprio eixo ).
Para pensar onde elas se encontram basta jogar os valores das retas na equação do logaritmo:
Os pontos de interseção serão e . O esboço de vai ficar assim:
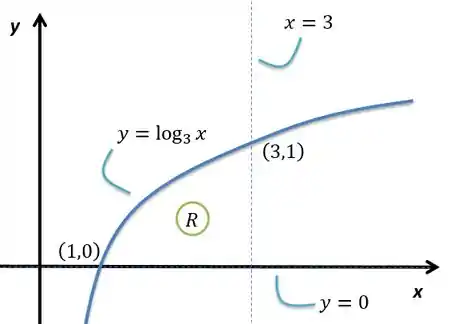
Passo 2
Vou redesenhar a região com o eixo de rotação:
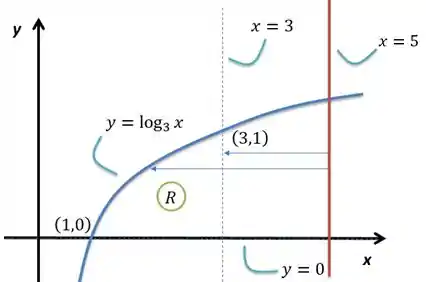
Repara, a seta de cima representa a distância até o pedaço que limita a região pelo lado mais perto do eixo, a maior seta limita pelo lado mais longe. A rotação da região em torno desse eixo é a mesma coisa que a rotação da logarítmica em torno desse eixo menos a rotação da reta , que vai gerar um cilindro. Pela situação, vou optar pelo método das seções transversais, que parece que vai ter uma integral mais fácil. Para isso tenho que inverter a função e chamar de raio a distância de cada uma das curvas até o eixo . O da região limita-se de até , dessa forma:
Onde,
Passo 3
Resolvendo: