UFMG, Sem Campus, Cálculo 3, Listas de Cálculo 3 - UFMG - Lista 1 - Integrais Duplas e Triplas, Questão 18
Calcule, utilizando coordenadas esféricas, o volume do sólido , limitado abaixo pelo plano e acima pela esfera
Passo 1
Eaew, belezinha?
O enunciado pede para calcularmos o volume delimitado pelas superfícies
e
para isso vamos ter que calcular a seguinte integração
em que delimita a nossa região! O enunciado pede para utilizarmos coordenadas esféricas! Vamos tentar visualizar a região e encontrar os limites de integração!
Passo 2
A região é dada por
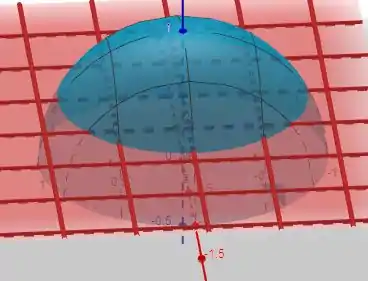
em que o plano em vermelho indica , com . E, superiormente temos a esfera . Vamos usar as coordenadas cilíndricas da forma
a nossa esfera é então descrita como
elevando ambos os lados ao quadrado, temos que
o que coloca o nosso raio como
em que usei que . A equação do plano nos dá que
Portanto, temos um valor mínimo para como
enquanto, temos que , deve começar em e ir até o momento em que o plano e a esfera se interceptam, ou seja, quando , de forma que
De forma que temos que resolver a seguinte integral
Vamos começar a integrar! Bora lá!
Passo 3
Precisamos integrar primeiro em já que seus limites são funções das outras variáveis, portanto, vamos resolver
para resolver esta integral podemos usar a regrinha
obtemos então que
Substituindo o resultado em nosso volume, obtemos que
Bora resolver a integração em agora! Bora Bora!
Passo 4
Podemos dividir nossa integral em duas da seguinte forma
A integral do primeiro termo pode ser identificada diretamente como
Agora, para a segunda integral é conveniente fazer a substituição simples
e
de forma que obtemos
em que usei e , temos que
ou simplesmente
Nosso volume se torna então
Estamos quase lá! Vamos resolver a última integral que falta!
Passo 5
A integral em pode ser identificada diretamente como
Obtemos então para o nosso volume
Vamos precisar reescrever um pouco isso para obter a nossa resposta! Vamos distribuir o produto do segundo termo, temos que
isso é equivalente à
A questão foi isso! Te vejo na próxima! Tchau Tchau!