UFJF – Cálculo 3 – Listas de Estudos – AV1 – 2022/2
5. Calcule o volume do sólido limitado inferiormente pelo cone , de equação , e superiormente pelo paraboloide , de equação
Passo 1
Falaaa... beleza??
Nessa questão vamos calcular o volume do sólido limitado inferiormente pelo cone de equação e superiormente de equação
Como estamos falando de volume de sólido, já pensamos em integral tripla.
Fazendo um esboço desse sólido:
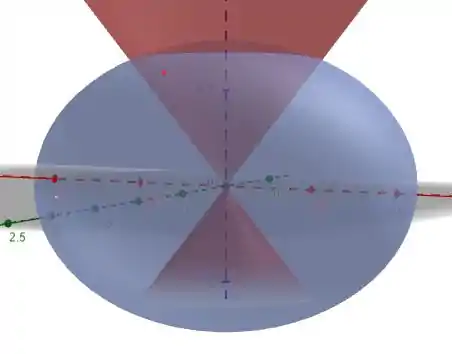
Como tem uma simetria tooooda em relação ao eixo , vamos usar coordenadas cilíndricas:
E para o jacobiano temos:
E o volume fica:
Passo 2
Pra achar a variação de , vamos usar as duas equações:
Substituindo o da primeira na segunda:
Usando as coordenas cilíndricas:
Então o varia de ate 1/2.
Passo 3
Como o sólido é limitado inferiormente pelo cone, isolamos o :
Usando as coordenadas cilíndricas:
E limitado superiormente pelo paraboloide, isomamos o :
Usando as coordenadas cilíndricas:
Passo 4
Agora podemos montar a integral tripla em coordenadas cilíndricas pra calcular o volume do sólido formado (não esquecendo do jacobiano)