Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volume pelas Seções Transversais

Ver Teoria
Exercício 912345678101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 2ª Lista, Questão 9

Sólido do primeiro octante, delimitado pelos planos x = 0 ,   y = 0 , pela esfera x 2 + y 2 + z 2 = 6 , situado entre os cones z = x 2 + y ² e 2 z = x 2 + y ²

Passo 1

Fala aí galera, bora resolver o nosso exercício? Vamos lá, começaremos destacando aqui todas as regiões delimitadas: pegar aqui a nossa integral tripla:

x = 0

y = 0

x 2 + y 2 + z 2 = 6

z = x 2 + y ²

2 z = x 2 + y ²

Se a gente tentar fazer um esboço disso, vamos ter algo parecido com:

No caso, o volume que queremos é justamente daquele pedacinho em vermelho.

Porém, a gente precisa olhar com foco nos eixos x e y para saber como será a variação deles. Para isso, a gente precisa encontrar a equação do círculo que forma na intercepção da esfera com os cones.

No primeiro cone:

z = x 2 + y ² → x 2 + y 2 = z ²

x 2 + y 2 + z 2 = 6

x 2 + y 2 + x 2 + y ² = 6

x 2 + y 2 = 3

Para o segundo cone:

2 z = x 2 + y ² → x 2 + y 2 4 = z ²

x 2 + y 2 + z 2 = 6

x 2 + y 2 + x 2 + y 2 4 = 6

5 x 2 + 5 y 2 4 = 6 → x 2 + y 2 = 24 5

Se a gente olhar para o plano x y , vamos achar:

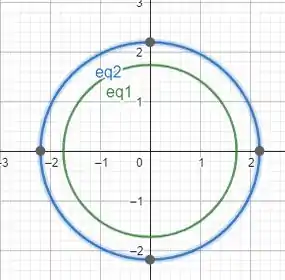
Como a gente quer somente o primeiro octante:

Passo 2

Show, agora vamos começar a montar a nossa integral. Para isso, vamos usar coordenadas esféricas:

x = p s e n ω c o s ⁡ ( θ )

y = p s e n ω s e n θ

z = p c o s ( ω )

J = p ² s e n ( ω )

Para entender como cada mudança vai funcionar:

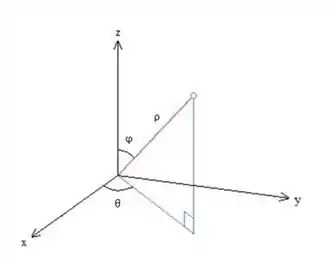
Começando por θ. Como o nosso sólido está no primeiro octante:

0 ≤ θ ≤ π 2

Agora para p . Como o nosso raio vai da origem até o limite da esfera, podemos dizer:

0 ≤ p ≤ 6

Agora, para entendermos como vai ser a variação de ω:

z = x 2 + y ²

Ficando:

p c o s ω = p s e n ω cos ⁡ θ 2 + ( p s e n ω s e n θ ) ²

p c o s ω = p ² s e n ² ω cos 2 ⁡ θ + p ² s e n ² ω s e n ² θ

p c o s ω = p s e n ω

t a n ω = 1 → ω = π 4

Analisando agora com o segundo cone:

2 z = x 2 + y ²

Ficando:

2 p c o s ω = p s e n ω cos ⁡ θ 2 + ( p s e n ω s e n θ ) ²

2 p c o s ω = p ² s e n ² ω cos 2 ⁡ θ + p ² s e n ² ω s e n ² θ

2 p c o s ω = p s e n ω

t a n ω = 2 → ω = H

Ué, mas nos achamos um ângulo H? Calma, lá na frente você vai entender qual a ideia por trás desse H .

Logo, teremos a integral:

∫ 0 6 ∫ 0 π 2 ∫ π 4 π 3 p ² s e n ( ω ) d ω d θ d p

Passo 3

Show, agora podemos calcular a nossa integral

∫ 0 6 ∫ 0 π 2 ∫ π 4 H p ² s e n ( ω ) d ω d θ d p

Vamos começar pela mais interna:

∫ π 4 H p ² s e n ( ω ) d ω = - p ² c o s ⁡ ( ω ) π 4 H

∫ π 4 H p 2 s e n ω d ω = - p 2 cos ⁡ H - cos ⁡ π 4

Ok, mas afinal de contas. Como a gente se livra desse H ? Bom, se liga, para isso vamos traçar o nosso plano cartesiano com o valor da tangente que tínhamos achado:

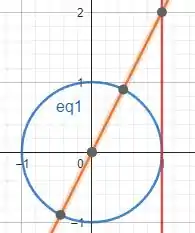
Reparem que a nossa reta vermelha é o valor da nossa tangente. O circulo trigonométrico tem raio igual a 1. Logo, reparem que temos um triângulo retângulo

Vamos começar achando o valor da hipotenusa:

h 2 = 2 2 + 1 2 = 5

h = 5

Ok, mas lembra que queremos o ângulo H ? Esse ângulo é justamente o ângulo formado entre a hipotenusa e o eixo x . Como já sabemos o valor do cateto e da hipotenusa:

c o s ⁡ ( H ) = c o s ⁡ ( ω ) = 1 5

Logo:

∫ π 4 H p 2 s e n ω d ω = - p 2 1 5 - 1 2

Ficando agora:

∫ 0 6 ∫ 0 π 2 - p 2 1 5 - 1 2 d θ d p = 1 2 - 1 5 ∫ 0 6 ∫ 0 π 2 p 2 d θ d p

Vamos continuar derivando em relação a mais interna:

∫ 0 π 2 p 2 d θ = p 2 θ 0 π 2

∫ 0 π 2 p 2 d θ = p 2 π 2

Ficando agora:

1 2 - 1 5 ∫ 0 6 p 2 π 2 d p = π 1 2 - 1 5 ∫ 0 6 p 2 d p

Derivando a última integral:

π 2 1 2 - 1 5 ∫ 0 6 p 2 d p = π 2 1 2 - 1 5 1 3 p 3 0 6

∫ 0 6 p 2 d p = π 2 1 2 - 1 5 1 3 6 3

∫ 0 6 p 2 d p = π 6 1 2 - 1 5

Resposta

π 6 1 2 - 1 5

Exercícios de Livros Relacionados

58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d