Dois cilindros circulares retos de raio r têm eixos que se intersectam em ângulos retos. Encontre o volume do sólido comum a ambos (Sugestão: Um oitavo do sólido está esboçado na figura abaixo).
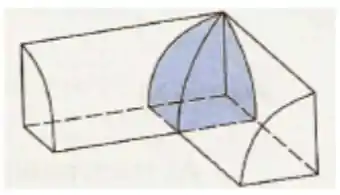
Passo 1
Essa questão assusta um pouco porque estamos falando de fatiamento de um sólido gerado por interseção. Relaxa no entanto, que com tranquilidade a gente chega lá. Pra começar, vamos estabelecer eixos:
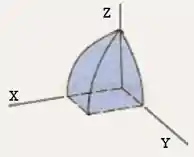
Note o seguinte, como o sólido foi montado a partir de cilindros iguais, então já sabemos o tamanho de todas as retas dentro da figura acima:
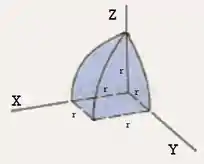
Show, agora vamos fazer uma seção transversal nessa figura. Note que se o corte for perpendicular ao eixo ...:
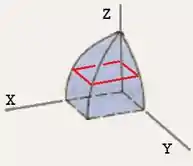
... então todas as seções transversais serão quadradas assim como é a base da figura! Como a área de um quadrado é dada por:
Somando os infinitos quadrados que definem esse sólido, temos então o volume do mesmo:
E como o quadrado tem área diferente dependendo da altura de corte , vamos ter:
Basta então modelar e achar os limites de integração pra poder partir pro abraço, beleza? Vamos nessa então!
Passo 2
Pra modelar eu vou destacar um pedacinho muito importante do sólido, esse aqui ó:
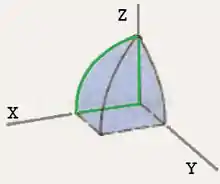
Destacando esse pedaço e exibindo a altura de corte vamos ter:
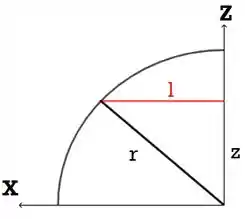
Opa, quer dizer então que dá pra usar Pitágoras? É isso mesmo! Vamos ter:
Como o volume é:
E vai da origem até seu valor máximo, o valor do raio , fechamos a modelagem da integral, que fica:
Fazendo as contas:
Como lá do enunciado vimos que o sólido da imagem é, na verdade, do sólido total e até agora mexemos só com o sólido da imagem, basta a gente multiplicar o resultado acima por e logo: