UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 6.2.2
Determine o volume do sólido gerado pela rotação, em torno do eixo , da região limitada pela curva e pelas retas , e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar o volume do sólido gerado pela rotação, em torno do eixo , da região limitada pela curva e pelas retas , e . Mas que região é essa? Vamos dar uma olhadinha no gráfico:
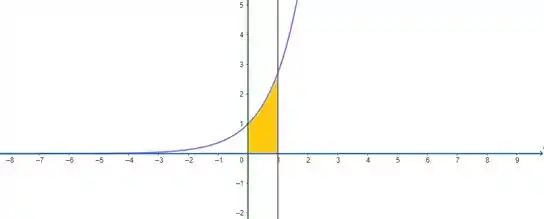
Nossa região é essa aí em amarelo e é ela que vai girar em torno do eixo . Nesses casos, de rotação em torno do eixo , nós podemos usar o método dos anéis para calcular o volume de rotação da região na forma:
Repara que , mas na fórmula temos um . Então, temos que escrever em função de . Além disso, repare que o raio externo do nosso anel é a distância de até o eixo, então vamos usar essa diferença no integrando.
Vamos lá!
Passo 2
No método dos anéis, a gente sempre tem que considerar o raio externo menos o raio interno. Como a gente já viu, é o nosso raio externo, ele vai tá variando de até a interseção com a curva , que vai acontecer em . Então, temos .
E o nosso raio interno vai ser dado pela curva em função de , ou seja:
Isso porque o logaritmo é a função inversa da exponencial, beleza? Repare no gráfico que a curva começa em e vai até , na região em amarelo.
Juntando todas essas informações, podemos escrever nossa integral para o volume de rotação na forma:
Então, integramos uma constante na primeira integral e, usando integração por partes na segunda, encontramos:
Aplicando os intervalos de integração:
Como e , temos:
Valeu, galera! Até a próxima! 😉