Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volume pelas Seções Transversais

Ver Teoria
Exercício 105123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UNICAMP – Cálculo 1 – Professor Ricardo Martins – Lista de Integrais

9.7 Seja R a região entre os gráficos de y = x e y = x 2 . Seja S x o sólido obtido girando R em torno do eixo x e S y o sólido obtido girando R em torno do eixo y . Calcule os volumes de S x e de   S y .

Passo 1

Falaaa tudo bem??

Nessa questão vamos calcular o volume de S x , o sólido obtido girando R em torno do eixo x , e o volume de S y , o solido obtido girando R em torno do eixo y .

A região R é a delimitada pelos gráficos de y = x e y = x 2 .

Pra quando é em torno de x , usamos:

S x = ∫ a b π f 2 x 2 - f 1 x 2 d x

Onde a e b são os limites em x . f 2 é a função que está mais acima e f 1 é a função que está mais abaixo.

Pra quando é em torno de y , usamos:

S y = ∫ a b π f 2 y 2 - f 1 y 2 d y

Onde a e b são os limites em y . f 2 é a função que está mais pra direita e f 1 é a função que está mais à esquerda.

Passo 2

Vamos esboçar os gráficos das duas funções:

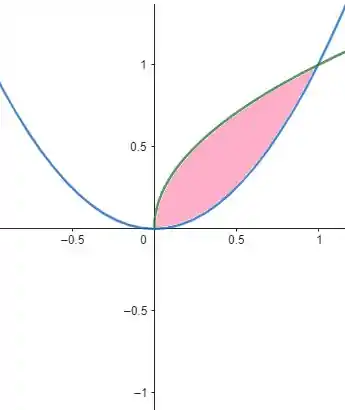
Temos a função y = x 2 em azul e a função y = x em verde.

Pra achar os pontos de interseção igualamos as duas funções:

x 2 = x

x 4 = x

x 4 - x = 0

x x 3 - 1 = 0

x x - 1 x 2 + x + 1 = 0

Temos:

x = 0

x - 1 = 0

x 2 + x + 1 = 0

Vamos pegar somente as raízes reais:

x = 0 → y = 0

x = 1 → y = 1

Passo 3

Pra calcular o volume da revolução em torno do eixo x :

S x = ∫ a b π f 2 x 2 - f 1 x 2 d x

S x = ∫ 0 1 π x 2 - x 2 2 d x

S x = π ∫ 0 1 x - x 4 d x

S x = π x 2 2 - x 5 5 0 1

S x = π 1 2 - 1 5

S x = 3 π 10

Passo 4

Pra calcular o volume da revolução em torno do eixo y :

S y = ∫ a b π f 2 y 2 - f 1 y 2 d y

Como f 2 x = y = x , então f 2 y = y 2 e como f 1 x = y = x 2 , então f 1 y = y .

Maaas quem está mais pra direita é a f 1 x .

S y = ∫ 0 1 π y 2 - y 2 2 d y

S y = π ∫ 0 1 y - y 4 d y

S y = π ∫ 0 1 y - y 4 d y

S y = π y 2 2 - y 5 5 0 1

S y = π 1 2 - 1 5

S y = 3 π 10

Resposta

S x = 3 π 10

S y = 3 π 10

Exercícios de Livros Relacionados

58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d