O volume do sólido limitado por e é
Passo 1
Olá meu caro amigo, como você está? Espero que esteja bem pois agora iremos resolver uma querida integral. Queremos calcular o volume de um solido, e uma forma interessante de fazer isso é com integrais triplas. Vamos da uma olhada no solido que a gente precisa calcular o volume.
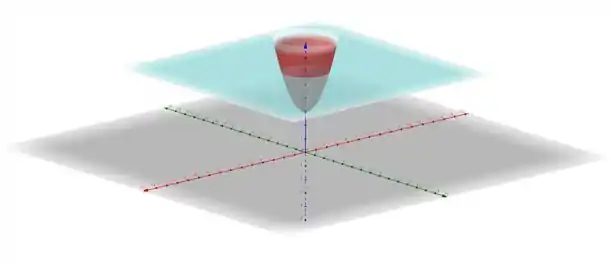
Para facilitar a minha vida e a sua vida, vamos parametrizar essa figura?
Vamos utilizar as coordenadas cilíndricas nesse caso, onde
Os nossos queridos intervalos,
Passo 2
Agora é a hora de lançar a braba, montar a integral e calcular